Bài tập 15 trang 104 SBT Toán 9 Tập 1
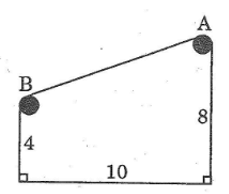
Giữa hai tòa nhà (kho và phân xưởng) của một nhà máy, người ta xây dựng một băng chuyền AB để chuyển vật liệu. Khoảng cách giữa hai tòa nhà là 10m, còn hai vòng quay của băng chuyền được đặt ở độ cao 8m và 4m so với mặt đất. Tìm độ dài AB của băng chuyền.
Hướng dẫn giải chi tiết
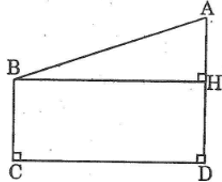
Kẻ BH ⊥ AD ta được tứ giác BCDH là hình chữ nhật.
Ta có: BC = DH và BH = CD (tính chất hình chữ nhật)
Suy ra: DH = 4(cm)
AH = 8 – 4 = 4 (cm)
BH = 10 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:
AB2 = BH2 + AH2
Suy ra: AB ≈ 10,8 (m)
Vậy băng chuyền dài khoảng 10,8 m.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 13 trang 104 SBT Toán 9 Tập 1
Bài tập 14 trang 104 SBT Toán 9 Tập 1
Bài tập 16 trang 104 SBT Toán 9 Tập 1
Bài tập 17 trang 104 SBT Toán 9 Tập 1
Bài tập 18 trang 105 SBT Toán 9 Tập 1
Bài tập 19 trang 105 SBT Toán 9 Tập 1
Bài tập 20 trang 105 SBT Toán 9 Tập 1
Bài tập 1.1 trang 105 SBT Toán 9 Tập 1
Bài tập 1.2 trang 105 SBT Toán 9 Tập 1
Bài tập 1.3 trang 105 SBT Toán 9 Tập 1
Bài tập 1.4 trang 105 SBT Toán 9 Tập 1
Bài tập 1.5 trang 105 SBT Toán 9 Tập 1
Bài tập 1.6 trang 106 SBT Toán 9 Tập 1
Bài tập 1.7 trang 106 SBT Toán 9 Tập 1
Bài tập 1.8 trang 106 SBT Toán 9 Tập 1
-


Chứng minh AH^3 = BE . CF . BC
bởi Mai Rừng
 23/01/2019
23/01/2019
Cho tam giác ABC, góc A = 90 độ, \(AH\perp BC\), kẻ \(HE\perp AB\) ( E thuộc AB), \(HF\perp AC\) (F thuộc AC). Chứng minh:
1) \(AH^3=BE.CF.BC\)
2) \(HE.BC+HF.BC=AH.BC\)
3) \(\dfrac{1}{HE^2}+\dfrac{1}{HC^2}=\dfrac{1}{HF^2}+\dfrac{1}{HB^2}\)
4) \(\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
5) Gọi M là trung điểm BC, chứng minh: \(AM\perp EF\)
6) Cho BC=5cm. Tìm GTLN của BH.CH; GTLN của \(AB^2+AC^2\)
7) CHứng minh: \(\sqrt{BH.CH}\le\dfrac{BC}{2}\)
Theo dõi (0) 1 Trả lời -


Nêu cách tính cạnh còn lại của tam tam giác vuông mà không dùng định lí py ta go
bởi Nguyễn Thanh Trà
 19/09/2018
19/09/2018
Cách tính cạnh còn lại của tam giác vuông 3 cạnh mag không sử dụng định lí ly ta go
Theo dõi (0) 1 Trả lời -


1)Cho \(\alpha\)là góc nhọn.Rút gọn bt:
\(A=\sin^6\alpha+cos^6\alpha+3sin^2\alpha-cos^2\alpha\)
2)Cho tam giác ABC vuông tại A.C/m:\(\tan\dfrac{B}{2}=\dfrac{AC}{AB+BC}\)
3)Cho tam giác ABC,A=90,đ/cao AH.Gọi I và K thứ tự là hình chiếu của H trên AB,AC.Đặt AB=x.AC=y
a)Tính AI,AK theo x và y
b)CMR:\(\dfrac{BI}{CK}=\dfrac{x^3}{y^3}\)
GIÚP MK VS MK THANKS NHÌU Ạ
Theo dõi (0) 1 Trả lời