Bài tập 10 trang 157 SBT Toán 9 Tập 1
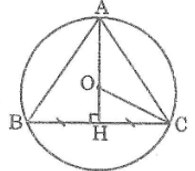
Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng:
A. 2\(\sqrt 3 \) cm
B. 2cm
C. \(\sqrt 3 \) cm
D. \(\sqrt 2 \) cm
Hướng dẫn giải chi tiết
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
Vậy chọn đáp án C.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 8 trang 157 SBT Toán 9 Tập 1
Bài tập 9 trang 157 SBT Toán 9 Tập 1
Bài tập 11 trang 157 SBT Toán 9 Tập 1
Bài tập 12 trang 158 SBT Toán 9 Tập 1
Bài tập 13 trang 158 SBT Toán 9 Tập 1
Bài tập 14 trang 158 SBT Toán 9 Tập 1
Bài tập 1.1 trang 158 SBT Toán 9 Tập 1
-
Bài 7 trang 157 sách bài tập toán 9 tập 1
bởi Dell dell
10/10/2018
Bài 7 (Sách bài tập trang 157)
.jpg)
Hình 73
Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy. Làm thế nào để xác định được bán kính của đường viền ?
Theo dõi (0) 1 Trả lời -
Bài 5 trang 156 sách bài tập toán 9 tập 1
bởi Lê Tấn Thanh
26/09/2018
Bài 5 (Sách bài tập trang 156)Trong các câu sau, câu nào đúng ? Câu nào sai ?
a) Hai đường tròn phân biệt có thể có hai điểm chung
b) Hai đường tròn phân biệt có thể có ba điểm chung phân biệt
c) Tâm của đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác ấy
Theo dõi (0) 1 Trả lời -
Bài 4 trang 156 sách bài tập toán 9 tập 1
bởi Nguyễn Hiền
26/09/2018
Bài 4 (Sách bài tập trang 156)Cho góc nhọn xOy và hai điểm D, E thuộc tia Oy. Dựng đường tròn tâm M đi qua D và E sao cho tâm M nằm trên tia Ox ?
Theo dõi (0) 1 Trả lời
