Bài tập 13 trang 158 SBT Toán 9 Tập 1
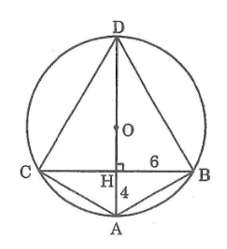
Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC
Hướng dẫn giải chi tiết
Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì tam giác ABC cân tại A nên AH là đường trung trực của BC. Suy ra AD là đường trung trực của BC.
Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC.
Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra góc (ACD) = 90o.
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: CH2 = HA.HD
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Trục đối xứng của đường tròn???
bởi Nguyễn Thị Lưu
 25/07/2018
25/07/2018
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Theo dõi (0) 0 Trả lời -


Cách xác định đường tròn
bởi Nguyễn Thanh Trà
 24/07/2018
24/07/2018
Sao để xác định đường tròn các bạn nhỉ?
Theo dõi (0) 2 Trả lời