Vận dụng 3 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT

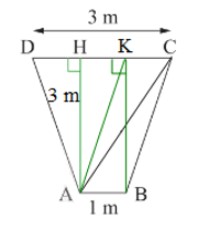
Xét hình thang cân ABCD (AB // DC) có $\widehat{D}=\widehat{C}$; AD = BC và AC = BD (tính chất hình thang cân).

Kẻ BK ⊥ DC.

Ta có AB // DC và BK ⊥ DC

Suy ra BK ⊥ AB nên $\widehat{ABK}=90°$.

Xét ∆AHK và ∆ABK có:

$\widehat{KHA}=\widehat{ABK}=90°$;

AK là cạnh chung;

$\widehat{AKH}=\widehat{KAB}$ (hai góc so le trong của DC // AB).

Do đó ∆AHK = ∆ABK (cạnh huyền – góc nhọn)

Suy ra HK = BK = 1 m (hai cạnh tương ứng).

Xét ∆AHD và ∆BKC có:

$\widehat{AHD}=\widehat{BKC}=90°$;

AD = BC (chứng minh trên);

$\widehat{D}=\widehat{C}$ (chứng minh trên).

Do đó ∆AHD = ∆BKC (cạnh huyền – góc nhọn).

Suy ra DH = CK (hai cạnh tương ứng).

Mà DH + HK + CK = DC

Hay 2DH = DC – HK

Khi đó DH = CK = $\frac{DC-HK}{2}$ = $\frac{3-1}{2}$ = 1 (m) và HC = 2 m.

Áp dụng định lí Pythagore cho DAHD vuông tại H, ta có:

AD² = AH² + DH² = 3² + 1² = 9 + 1 = 10.

Do đó AD = $\sqrt{10}$ (m).

Áp dụng định lí Pythagore cho ∆AHC vuông tại H, ta có:

AC² = AH² + HC² = 3² + 2² = 9 + 4 = 13.

Do đó AC = $\sqrt{13}$ (m).

Vậy AD = BC = $\sqrt{10}$ m, AC = BD = $\sqrt{13}$ m.

-- Mod Toán 8 HỌC247