Bài 4 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT

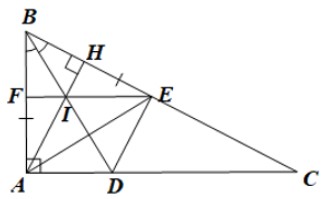
a) Xét ∆ABD và ∆EBD có:

BA = BE (giả thiết);

$\widehat{ABD}=\widehat{EBD}$ (do BD là tia phân giác của $\widehat{ABE}$);

BD là cạnh chung,

Do đó ∆ABD = ∆EBD (c.g.c).

b) Do ∆ABD = ∆EBD (câu a) nên $\widehat{BAD}=\widehat{BED}=90°$ (hai góc tương ứng).

Do đó DE ⊥ BC

Mà AH ⊥ BC (giả thiết) nên DE // AH.

Tứ giác ADEH có DE // AH nên là hình thang

Lại có $\widehat{AHE}=90°$ nên ADEH là hình thang vuông.

c) Do ∆ABD = ∆EBD (câu a) nên AD = ED (hai cạnh tương ứng)

Do đó D nằm trên đường trung trực của AE.

Lại có BA = BE (giả thiết) nên B nằm trên đường trung trực của AE.

Suy ra BD là đường trung trực của đoạn thẳng AE nên BD ⊥ AE, hay BI ⊥ AE.

Xét ∆ABE có AI ⊥ BE, BI ⊥ AE nên I là trực tâm của tam giác

Do đó EI ⊥ AB hay EF ⊥ AB.

Mà CA ⊥ AB (do ∆ABC vuông tại A)

Suy ra EF // CA.

Tứ giác ACEF có EF // CA nên là hình thang.

Lại có $\widehat{FAC}=90°$ nên ACEF là hình thang vuông.

-- Mod Toán 8 HỌC247