Khám phá 3 trang 83 SGK Toán 8 Chân trời sáng tạo Tập 1
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu là góc vuông thì và cũng là góc vuông.
b) Nếu AC = BD thì vuông.
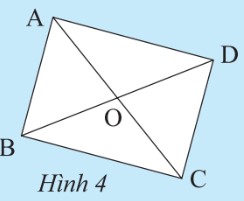
Hướng dẫn giải chi tiết Khám phá 3
a) Do \(ABCD\) là hình bình hành nên \(AB // CD\) và \(AD // BC\).
Do là góc vuông nên AD ⊥ AB.
Ta có:
- \(AB // CD\) và AD ⊥ AB nên AD ⊥ CD hay là góc vuông;
- \(AD // BC\) và AD ⊥ AB nên BC ⊥ AB hay là góc vuông.
b) Hình bình hành \(ABCD\) có \(AB // CD\) nên cũng là hình thang có hai cạnh đáy là AB và CD.
Lại có hai đường chéo \(AC = BD\) nên là hình thang cân.
Do đó và .
Tương tự ta cũng có
Suy ra
Mà
Hay , do đó .
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Thực hành 1 trang 83 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Vận dụng 1 trang 83 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Thực hành 2 trang 84 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Vận dụng 2 trang 84 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Khám phá 4 trang 84 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Khám phá 5 trang 85 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Thực hành 3 trang 85 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Vận dụng 3 trang 85 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Khám phá 6 trang 85 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Khám phá 7 trang 86 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Thực hành 4 trang 86 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Vận dụng 4 trang 86 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 1 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 2 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 3 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 4 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 5 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


