Thực hành 4 trang 86 SGK Toán 8 Chân trời sáng tạo Tập 1
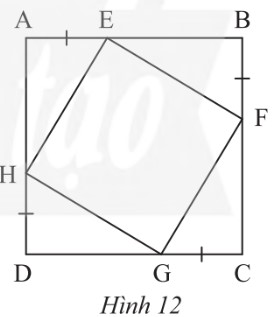
Trong Hình 12, cho biết ABCD là một hình vuông. Chứng minh rằng:
a) Tứ giác EFGH có ba góc vuông;
b) HE = HG;
c) Tứ giác EFGH là một hình vuông.
Hướng dẫn giải chi tiết Thực hành 4
a) Do ABCD là một hình vuông nên và \(AB = BC = CD = DA\).
Mà \(AE = BF = CG = DH\) nên \(EB = FC = GD = HA\).
Xét \(\Delta{AEH}\) và \(\Delta{DGH}\) có:
; \(AE = GH; AH = DG\)
Do đó \(\Delta{AEH} = \Delta{AEH}\) (hai cạnh góc vuông)
Suy ra (hai góc tương ứng).
Xét \(\Delta{AEH}\) có (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Do đó hay
.
Khi đó là một góc vuông.
Chứng minh tương tự ta cũng có là một góc vuông.
Vậy tứ giác \(EFGH\) có ba góc vuông.
b) Do \(\Delta{AEH} = \Delta{DHG}\) (câu a)
Suy ra \(HE = HG\) (hai cạnh tương ứng).
c) Chứng minh tương tự câu b, ta cũng có: \(HE = EF, HE = FG\).
Khi đó tứ giác \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi.
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật.
Tứ giác \(EFGH\) vừa là hình thoi vừa là hình chữ nhật nên là hình vuông.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Khám phá 6 trang 85 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Khám phá 7 trang 86 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Vận dụng 4 trang 86 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 1 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 2 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 3 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 4 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Bài 5 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





