Bài 3 trang 87 SGK Toán 8 Chân trời sáng tạo Tập 1 - CTST

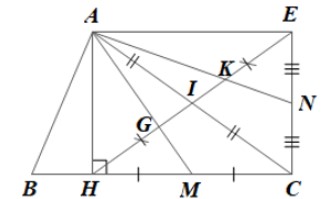
a) Do E là điểm đối xứng với H qua I nên I là trung điểm của HE.

Tứ giác \(AHCE\) có hai đường chéo AC và HE cắt nhau tại trung điểm I của mỗi đường nên là hình bình hành.

Lại có $\widehat{AHC}=90°$ nên hình bình hành \(AHCE\) là hình chữ nhật.

b) Xét \(\Delta{AHC}\) có AM, HI là hai đường trung tuyến cắt nhau tại G nên G là trọng tâm của \(\Delta{AHC}\).

Suy ra $HG=\frac{2}{3}HI$ và $IG=\frac{1}{2}HG$.

Chứng minh tương tự đối với \(\Delta{AEC}\) có K là trọng tâm của \(\Delta{AEC}\).

Suy ra $EK=\frac{2}{3}EI$ và $IK=\frac{1}{2}EK$.

Ta có: $HG=\frac{2}{3}HI$, $EK=\frac{2}{3}EI$ và HI = EI nên $HG=EK\left(=\frac{2}{3}EI\right)$.

Lại có: $IG=\frac{1}{2}HG$ và $IK=\frac{1}{2}EK$ nên $IG=IK=\frac{1}{2}HG$

Mặt khác $GK=IG+IK=\frac{1}{2}HG+\frac{1}{2}HG=HG$.

Vậy \(HG = GK = KE\).

-- Mod Toán 8 HỌC247