Hoạt động 3 trang 102 SGK Toán 8 Tập 1 Cánh diều
Cho hình thang cân ABCD có AB // CD , AB < CD, E là giao điểm của AD và BC (Hình 25).
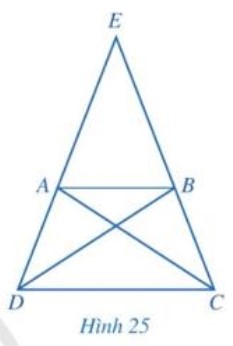
a) So sánh các cặp góc: \(\widehat {E{\rm{D}}C}\) và \(\widehat {EC{\rm{D}}}\); \(\widehat {E{\rm{A}}B}\) và \(\widehat {EBA}\).
b) So sánh các cặp đoạn thẳng: EA và EB, ED và EC. Từ đó, hãy so sánh AD và BC.
c) Hai tam giác ADC và BCD có bằng nhau hay không? Từ đó, hãy so sánh AC và BD.
Hướng dẫn giải chi tiết Hoạt động 3
a) Do ABCD là hình thang cân nên:
\(\widehat {ADC} = \widehat {BCD}\)hay \(\widehat {EDC} = \widehat {ECD}\)
Do ABCD là hình thang cân nên
\(\widehat {BAD} = \widehat {ABC}\left( 1 \right)\)
Mà:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = {180^0}\\\widehat {ABC} + \widehat {EBA} = {180^0}\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = \widehat {ABC} + \widehat {EBC}\\ \Rightarrow \widehat {EAB} = \widehat {EBA}\end{array}\)(do(1))
b) Do \(\widehat {EAB} = \widehat {EBA}\) suy ra \(\Delta EAB\) cân tại E nên EA = EB
Do \(\widehat {EDC} = \widehat {ECD}\) suy ra \(\Delta ECD\) cân tại E nên ED = EC
Mà: EA = EC
Suy ra EA + AD = EB + BC
Suy ra AD = BC (do EA = EB)
c) Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC
\(\widehat {ADC} = \widehat {BCD}\)
DC chung
Suy ra: \(\Delta ADC = \Delta BCD(c.g.c) \Rightarrow AC = BD\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Hoạt động 1 trang 101 SGK Toán 8 Tập 1 Cánh diều - CD
Hoạt động 2 trang 101 SGK Toán 8 Tập 1 Cánh diều - CD
Luyện tập 1 trang 102 SGK Toán 8 Tập 1 Cánh diều - CD
Hoạt động 4 trang 102 SGK Toán 8 Tập 1 Cánh diều - CD
Luyện tập 2 trang 103 SGK Toán 8 Tập 1 Cánh diều - CD
Bài 1 trang 103 SGK Toán 8 Tập 1 Cánh diều - CD
Bài 2 trang 104 SGK Toán 8 Tập 1 Cánh diều - CD
Bài 3 trang 104 SGK Toán 8 Tập 1 Cánh diều - CD
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


