Giải bài 33 tr 33 sách BT Toán lớp 8 Tập 1
Tính tích x, y , biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số) :
a. \(\left( {4{a^2} - 9} \right)x = 4a + 4\)với a ≠ \( \pm {3 \over 2}\) và \(\left( {3{a^3} + 3} \right)y = 6{a^2} + 9a\) với a ≠ − 1
b. \(\left( {2{a^3} - 2{b^3}} \right)x - 3b = 3a\)với a ≠ b và \(\left( {6a + 6b} \right)y = {\left( {a - b} \right)^2}\) với a ≠ − b
Chú ý rằng\({a^2} + ab + {b^2} = {a^2} + 2a.{b \over 2} + {{{b^2}} \over 4} + {{3{b^2}} \over 4} = {\left( {a + {b \over 2}} \right)^2} + {{3{b^2}} \over 4} \ge 0\).
Do đó nếu a ≠ 0 hoặc b ≠ 0 thì\({a^2} + ab + {b^2} > 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Muốn nhân hai phân thức, ta nhân các tử thức với nhau, nhân các mẫu thức với nhau.
Với \(B,D\ne 0\) ta có: \(\dfrac{A}{B}.\dfrac{C}{D} = \dfrac{{A.C}}{{B.D}}\)
Lời giải chi tiết
a. Vì a ≠ \( \pm {3 \over 2}\) nên\(4{a^2} - 9 \ne 0 \Rightarrow x = {{4a + 4} \over {4{a^2} - 9}}\)
Vì a ≠ − 1 nên \(3{a^3} + a \ne 0 \Rightarrow y = {{6{a^2} + 9a} \over {3{a^3} + a}}\)
Do đó: \(xy = {{4a + 4} \over {4{a^2} - 9}}.{{6{a^2} + 9a} \over {3{a^3} + 3}} = {{4\left( {a + 1} \right).3a\left( {2a + 3} \right)} \over {\left( {2a + 3} \right)\left( {2a - 3} \right).3\left( {{a^3} + 1} \right)}}\)
\( = {{4a\left( {a + 1} \right)} \over {\left( {2a - 3} \right)\left( {a + 1} \right)\left( {{a^2} - a + 1} \right)}} = {{4a} \over {\left( {2a - 3} \right)\left( {{a^2} - a + 1} \right)}}\)
b. Vì a ≠ b nên \(2{a^3} - 2{b^3} \ne 0 \Rightarrow x = {{3a + 3b} \over {2{a^3} - 2{b^3}}}\)
Vì a ≠ − b nên \(6a + 6b \ne 0 \Rightarrow y = {{{{\left( {a - b} \right)}^2}} \over {6a + 6b}}\)
Do đó: \(xy = {{3a + 3b} \over {2{a^3} - 2{b^3}}}.{{{{\left( {a - b} \right)}^2}} \over {6a + 6b}} = {{3\left( {a + b} \right){{\left( {a - b} \right)}^2}} \over {2\left( {{a^3} - {b^3}} \right).6\left( {a + b} \right)}}\)
\( = {{{{\left( {a - b} \right)}^2}} \over {4\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)}} = {{a - b} \over {4\left( {{a^2} + ab + {b^2}} \right)}}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Tính diện tích lúc đầu của miếng đất ?
bởi Tran Ngoc Phuong
 13/04/2020
Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 10m. Nếu giảm chiều dài đi 3m và tăng chiều rộng 15m thì diện tích miếng đất tăng 177m^2. Tính diện tích lúc đầu của miếng đất.CÁC BẠN GIÚP MÌNH GIẢI VỚI SẮP KIỂM TRA RỒI TT_TTTheo dõi (0) 2 Trả lời
13/04/2020
Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 10m. Nếu giảm chiều dài đi 3m và tăng chiều rộng 15m thì diện tích miếng đất tăng 177m^2. Tính diện tích lúc đầu của miếng đất.CÁC BẠN GIÚP MÌNH GIẢI VỚI SẮP KIỂM TRA RỒI TT_TTTheo dõi (0) 2 Trả lời -


Thực hiện phép tính (4x-1)/(3x^2y)-(7x-1)/3x^2y)
bởi Bé Thảo
 02/04/2020
E ko bt lm
02/04/2020
E ko bt lm Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Chứng minh rằng với mọi số tự nhiên m, ta có 4/(4m+2)=1/(m+1)+1/(m+1)(2m+1)
bởi Hoàng Thị Mai
 01/04/2020
.
01/04/2020
. Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Cho tứ giác ABCD gọi P, Q là trung điểm AB, CD. Gọi M, N là trung điểm 2 đường chéo AC, BD. Chứng minh MN, PQ cắt nhau tại trung điểm mỗi đường.
bởi Trang Nguyễn Thùy
 16/03/2020
Làm hộ câu 5 ạ!! Cảm ơn nhiều!!!
16/03/2020
Làm hộ câu 5 ạ!! Cảm ơn nhiều!!! Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -
ADMICRO


Tìm giá trị của biểu thức A khi x=3 : 2x(x-3)/x+3
bởi Vy Bùi
 29/02/2020
29/02/2020
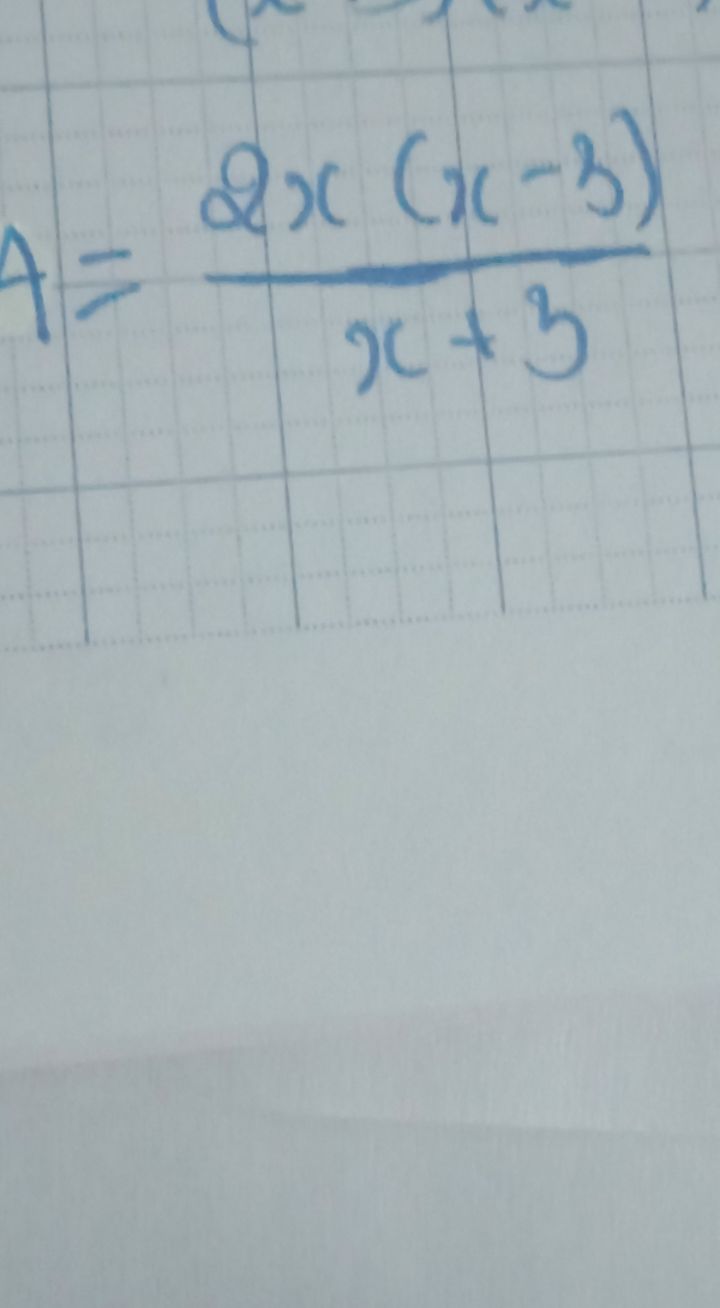 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Thực hiện phép tính 3x(x^2 x-1)
bởi Thùy Mily's
 01/01/2020
Trả lới giúp mik bài 1,2,3 luôn nha
01/01/2020
Trả lới giúp mik bài 1,2,3 luôn nha Theo dõi (1) 11 Trả lời
Theo dõi (1) 11 Trả lời -


Rút gọn phân thức x-2/x+1.x^2-2x-3/x^2-5x+6
bởi Lê Trung Phuong
 30/01/2019
30/01/2019
Rút gọn phân thức :
\(\dfrac{x-2}{x+1}.\dfrac{x^2-2x-3}{x^2-5x+6}\)
Theo dõi (0) 1 Trả lời


