Giải bài 29 tr 10 sách BT Toán lớp 8 Tập 2
Giải các phương trình sau:
a. \(\left( {x - 1} \right)\left( {{x^2} + 5x - 2} \right) - \left( {{x^3} - 1} \right) = 0\)
b. \({x^2} + \left( {x + 2} \right)\left( {11x - 7} \right) = 4\)
c. \({x^3} + 1 = x\left( {x + 1} \right)\)
d. \({x^3} + {x^2} + x + 1 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Phân tích vế trái thành nhân tử.
- Áp dụng phương pháp giải phương trình tích: \(A(x).B(x) = 0 ⇔ A(x) = 0\) hoặc \(B(x) = 0.\)
Lời giải chi tiết
a. \(\left( {x - 1} \right)\left( {{x^2} + 5x - 2} \right) - \left( {{x^3} - 1} \right) = 0\)
\(\eqalign{ & \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 5x - 2} \right) - \left( {x - 1} \right)\left( {{x^2} + x + 1} \right) = 0 \cr & \Leftrightarrow \left( {x - 1} \right)\left[ {\left( {{x^2} + 5x - 2} \right) - \left( {{x^2} + x + 1} \right)} \right] = 0 \cr & \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 5x - 2 - {x^2} - x - 1} \right) = 0 \cr & \Leftrightarrow \left( {x - 1} \right)\left( {4x - 3} \right) = 0 \cr} \)
\(\Leftrightarrow x - 1 = 0\) hoặc \(4x - 3 = 0\)
+ \(x - 1 = 0 \Leftrightarrow x = 1\)
+ \(4x - 3 = 0 \Leftrightarrow x = 0,75\)
Vậy phương trình có nghiệm x = 1 hoặc x = 0,75
b. \({x^2} + \left( {x + 2} \right)\left( {11x - 7} \right) = 4\)
\(\eqalign{ & \Leftrightarrow {x^2} - 4 + \left( {x + 2} \right)\left( {11x - 7} \right) = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left( {x - 2} \right) + \left( {x + 2} \right)\left( {11x - 7} \right) = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left[ {\left( {x - 2} \right) + \left( {11x - 7} \right)} \right] = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left( {x - 2 + 11x - 7} \right) = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left( {12x - 9} \right) = 0 \cr} \)
\( \Leftrightarrow x + 2 = 0\) hoặc \(12x - 9 = 0\)
+ \(x + 2 = 0 \Leftrightarrow x = - 2\)
+ \(12x - 9 = 0 \Leftrightarrow x = 0,75\)
Vậy phương trình có nghiệm x = -2 hoặc x = 0,75
c. \({x^3} + 1 = x\left( {x + 1} \right)\)
\(\eqalign{ & \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = x\left( {x + 1} \right) \cr & \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1} \right) - x\left( {x + 1} \right) = 0 \cr & \Leftrightarrow \left( {x + 1} \right)\left[ {\left( {{x^2} - x + 1} \right) - x} \right] = 0 \cr & \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1 - x} \right) = 0 \cr & \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - 2x + 1} \right) = 0 \cr & \Leftrightarrow \left( {x + 1} \right){\left( {x - 1} \right)^2} = 0 \cr} \)
\( \Leftrightarrow x + 1 = 0\) hoặc \({\left( {x - 1} \right)^2} = 0\)
+ \(x + 1 = 0 \Leftrightarrow x = - 1\)
+ \({\left( {x - 1} \right)^2} = 0 \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1\)
Vậy phương trình có nghiệm x = -1 hoặc x = 1
d. \({x^3} + {x^2} + x + 1 = 0\)
\(\eqalign{ & \Leftrightarrow {x^2}\left( {x + 1} \right) + \left( {x + 1} \right) = 0 \cr & \Leftrightarrow \left( {{x^2} + 1} \right)\left( {x + 1} \right) = 0 \cr} \)
\(\Leftrightarrow {x^2} + 1 = 0\) hoặc \(x + 1 = 0\)
+ \({x^2} + 1 = 0\) : vô nghiệm (vì \({x^2} \ge 0\) nên \({x^2} + 1 > 0\) )
+ \(x + 1 = 0 \Leftrightarrow x = - 1\)
Vậy phương trình có nghiệm x = -1
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Giải phương trình x^6-7x^3-8=0
bởi Huong Trịnh
 18/02/2020
lm giúp vs
18/02/2020
lm giúp vs Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm x biết (2x+5)^2 = (3x-1)^2
bởi Ngưu Kim
 18/02/2020
18/02/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình (2x+5)^2=(3x-1)^2
bởi Ngưu Kim
 18/02/2020
18/02/2020
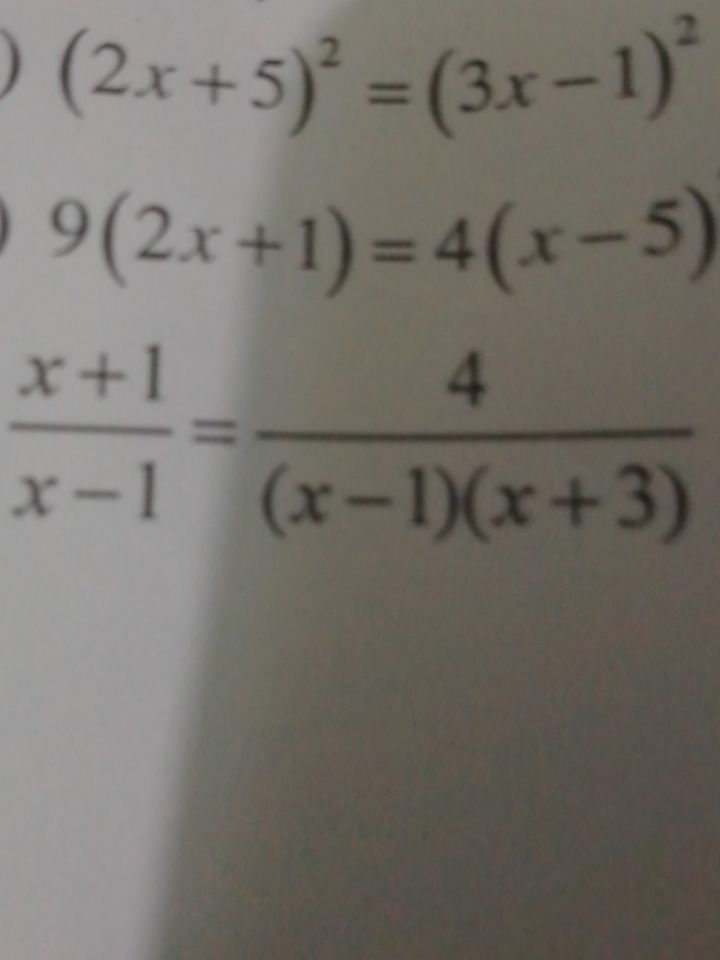 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x biết 2x^2-(4m+1)x 15-m=0
bởi Tỏi Củ
 17/02/2020
Mọi người giúp mình vớiTheo dõi (0) 0 Trả lời
17/02/2020
Mọi người giúp mình vớiTheo dõi (0) 0 Trả lời -
ADMICRO


Giải phương trình x^2-7x+10=0
bởi Lê Yến Nhi
 13/02/2020
13/02/2020
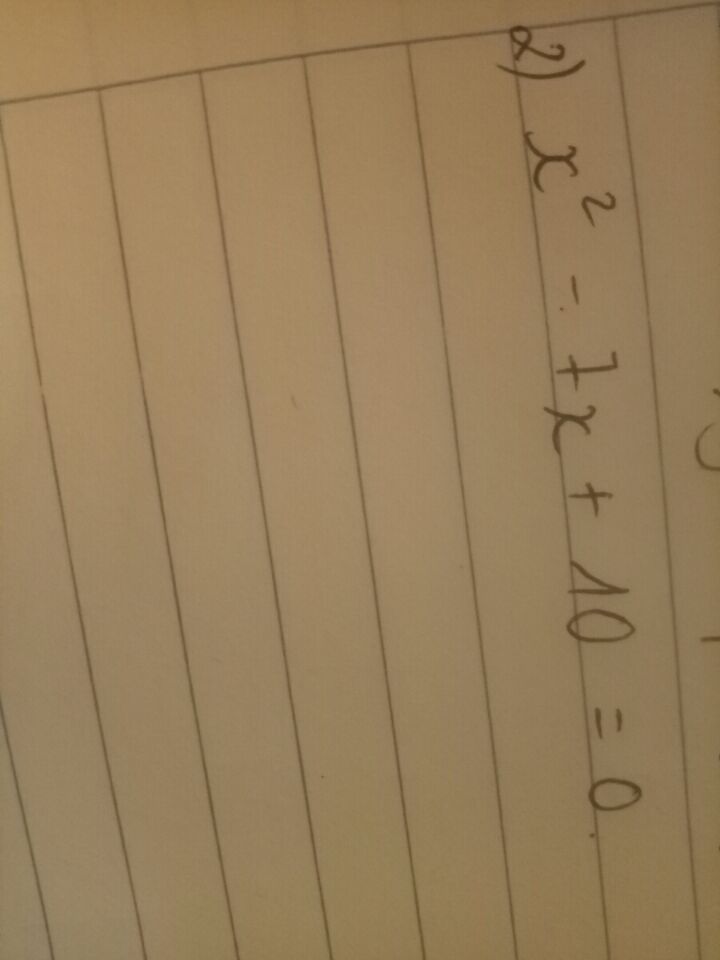 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm x biết x^2-3x+2=0
bởi phanh phanh
 12/02/2020
Câu 11
12/02/2020
Câu 11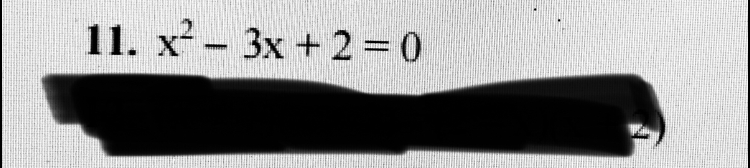 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm x biết x^2-x=0
bởi phanh phanh
 12/02/2020
Câu 10
12/02/2020
Câu 10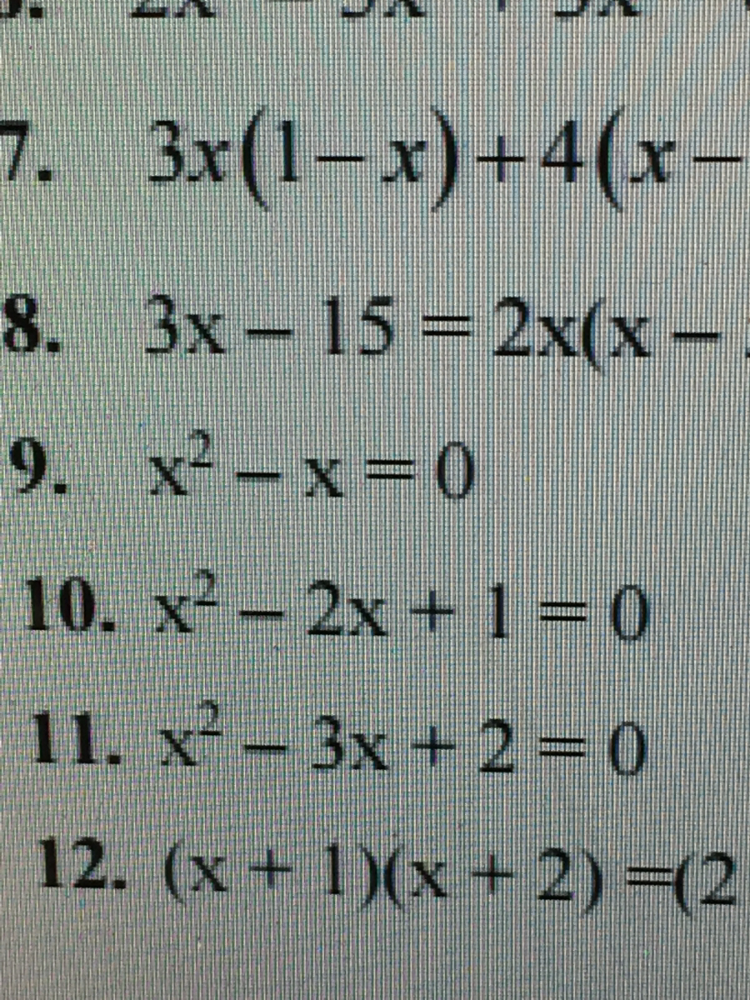 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x biết (x+1)^2+(x+5)=0
bởi Nguyễn Kiên
 11/02/2020
11/02/2020
(x+1)2+(x+5)=0
Theo dõi (1) 2 Trả lời -


Chứng tỏ 2x-3=2(x-3) vô nghiệm
bởi Nguyễn
 11/02/2020
Chứng tỏ các phương trình sau vô nghiệmTheo dõi (0) 6 Trả lời
11/02/2020
Chứng tỏ các phương trình sau vô nghiệmTheo dõi (0) 6 Trả lời -


Giải phương trình tích x(x+3)(x-3)-(x+2)(x^2 -2x+4)=0
bởi Lam Tịch Y
 09/02/2020
09/02/2020
a, x(x+3)(x-3)-(x+2)(x2 -2x+4)=0
b, 2x(x-3)+5(x-3)=0
Theo dõi (0) 1 Trả lời -


Tìm x biết (x^2+x+1)(6+2x)=0
bởi Trần Huy
 07/02/2020
07/02/2020
Tìm x biết (x^2+x+1)(6+2x)=0
Theo dõi (1) 1 Trả lời -


Tìm x biết (x^2 5x)^2-2(x^2 5x)=24
bởi Yến Nhi
 05/05/2019
(X^2 5x)^2-2(x^2 5x)=24Theo dõi (0) 1 Trả lời
05/05/2019
(X^2 5x)^2-2(x^2 5x)=24Theo dõi (0) 1 Trả lời -


Tìm x biết (x-1)(x+6) - (x-1)(x+1)=0
bởi Bảo Lộc
 17/11/2018
17/11/2018
(x-1)(x+6) - (x-1)(x+1)=0
Theo dõi (0) 1 Trả lời -


Tìm x biết (x^3+1)(x+2)=0
bởi Trịnh Lan Trinh
 17/11/2018
17/11/2018
(x^3+1)(x+2)=0
Theo dõi (0) 1 Trả lời -


Giải phương trình x^3 - 5x^2 + x - 5=0
bởi Dương Minh Tuấn
 17/11/2018
17/11/2018
giải phương trình tích
x3 - 5x2 + x - 5
Theo dõi (0) 1 Trả lời -


Giải phương trình tích (2x^2+1)(4x-3) = (2x^2+1)(x-12)
bởi Bánh Mì
 17/11/2018
17/11/2018
giải phương trình tích
(2x^2+1) * (4x-3) = (2x^2+1) * (x-12)
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức M = x^2−6x+2018
bởi Dell dell
 17/11/2018
17/11/2018
ÍM GTNN :
a) M = x2−6x+2018
b) N =x2−x
c) P =( x- 1) (x+3)
Theo dõi (0) 1 Trả lời -


Giải phương trình (x+1)2.(x+2)+(x-1)2(x-2)=12
bởi Phạm Khánh Ngọc
 17/11/2018
17/11/2018
Giải phương trình :
1) (x+1)2.(x+2)+(x-1)2(x-2)=12
2) (x-6)4 + (x-8)4 = 16
3) x4 + 3x3 + 4x2 + 3x + 1 = 0
4) (x2 - 1)(x2 + 4x + 3 ) = 192
Giúp mk nha các bạn CTV !
Theo dõi (0) 1 Trả lời -


Giải phương trình 3x^2-7x +8 =0
bởi hà trang
 17/11/2018
17/11/2018
giari cac phuong trinh tich
3x2-7x +8 =0
3x2+7x+2=0
4x2- 12x +9 =0
x2 -10x-2000
jup mk nhaTheo dõi (0) 1 Trả lời -


Tìm số tự nhiên x thỏa (x+2)(x+4)(x^2-9)=0
bởi Lê Thánh Tông
 15/09/2018
15/09/2018
Tìm \(x\in N\) thỏa mãn
\(\left(x+2\right)\left(x+4\right)\left(x^2-9\right)=0\)
Theo dõi (0) 1 Trả lời -


Tìm x, biết 7x(x-1)=x-1
bởi Nguyễn Trọng Nhân
 21/09/2018
21/09/2018
7x(x-1)=x-1
Theo dõi (0) 1 Trả lời -


Tìm x, biết x^2-6x+3-5(x+3)=0
bởi Lê Minh Hải
 21/09/2018
21/09/2018
x^2-6x+3-5(x+3)=0
Theo dõi (0) 1 Trả lời -


Tính quãng đường AB biết vận tốc nước 3km/h
bởi Nguyễn Sơn Ca
 29/09/2019
29/09/2019
1) 1 ca nô xuôi dòng từ bến sông A đến bến sông B hết 1 giờ 30 phút . Lúc về ngược dòng từ B đến A hết 2 giờ . Tính quảng đường AB . Biết vận tốc nước là 3km/h
2) 1 người đi bộ từ A đến B với vận tốc 6km/h. sau 3 giờ 1 người khác đi xe đạp với vận tốc 9km/h . Hỏi sau bao lâu kêr từ khi người đi bộ khởi hành thì hai người gặp nhau và gặp hau cách A bao nhiêu km
Theo dõi (0) 1 Trả lời -


Tìm x biết x^2+x-42=0
bởi My Le
 17/11/2018
17/11/2018
a)x2+x-42=0
b)3x2-10x+3
Theo dõi (0) 1 Trả lời -


Tìm x nguyên thỏa phương trình |x+1|(x^2-5)(x^2-4)=0
bởi Lê Nhi
 26/02/2019
26/02/2019
1. Tìm x thỏa mản phương trình x nguyên
\(\left|x+1\right|\left(x^2-5\right)\left(x^2-4\right)=0\)
2. Giải phương trình bậc 2
\(\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x^2-6x-7\right)}=0\)
3. Giải phương trình 2 ẩn
\(x^2-2xy+2y^2=0\)
4. Giải phương trình bậc 2 ẩn x
\(\dfrac{\left(x^2+5x-11\right)}{\left(x^2+11x-5\right)}\)
5. Tìm x, y thỏa mãn phương trình
\(\dfrac{x}{y}=\dfrac{1}{5}\)
\(x+y=7\)
6. Tìm x y biết x, y
\(\dfrac{y}{3}=\dfrac{x}{7}\)
\(x-y=6\)
Songoku giúp e vs mai là hết hạn
Theo dõi (0) 2 Trả lời -


Tim x, biết (x-3).(3x-9)=0
bởi Nguyễn Minh Minh
 13/10/2018
13/10/2018
tim x : (x-3) . (3x-9)=0
Theo dõi (0) 1 Trả lời -


Giải phương trình (x - 1)(x^2 + 3x -2) (x^3 - 1)= 0
bởi Xuan Xuan
 17/11/2018
17/11/2018
Giải phương trình
( x - 1)(x2 + 3x -2) - (x3 - 1)= 0
b) ( x3 + x2)+( x2 + x)=0
Theo dõi (0) 1 Trả lời -


Tìm n, biết 3^(n+2).(n-1)=1
bởi Bo Bo
 27/02/2019
27/02/2019
Tìm n, biết :
\(3^{\left(n+2\right)\left(n-1\right)}\)
Theo dõi (0) 3 Trả lời -


Tìm x biết 2x-8/6.3x+1/4=9x-2/8+3x-1/12
bởi Nguyễn Thị An
 26/12/2018
26/12/2018
\(\dfrac{2x-8}{6}\) -\(\dfrac{3x+1}{4}\) =\(\dfrac{9x-2}{8}\) +\(\dfrac{3x-1}{12}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình (x^2-9)(3x+2)=(9-x^2)(3-2x)
bởi Hy Vũ
 17/11/2018
17/11/2018
Giải PT sau :
(x^2-9)(3x+2)=(9-x^2)(3-2x)
Ai lm nhanh tick cho
Theo dõi (0) 1 Trả lời -


Tìm x biết x^15=x
bởi Lê Nhật Minh
 20/09/2018
20/09/2018
tìm x biết
x^ 15=x
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình (2x+1)(x+1)^2(2x+3)=18
bởi Lan Anh
 17/11/2018
17/11/2018
giải pt: (2x+1)(x+1)2(2x+3)=18
Theo dõi (0) 1 Trả lời -


Tìm x biết (3x+2)(x^2-1)=(9x^2-4)(x+1)
bởi Lê Thánh Tông
 17/11/2018
17/11/2018
a) (3x+2)(x^2-1)=(9x^2-4)(x+1)
b) (x+2)(3-4x)=x^2+4x+4
c) (2x-5)^2-(x+2)^2=0
d) (x^2-2x+1)-4=0
Theo dõi (0) 1 Trả lời -


Giải phương trình x(x+1)(x^2+x+1)=42
bởi Truc Ly
 17/11/2018
17/11/2018
Giải pt: x(x+1)(x2+x+1)=42
Theo dõi (0) 1 Trả lời -


Tìm x biết x(x-1)(x-4)(x+5)=84
bởi Lê Minh Trí
 17/11/2018
17/11/2018
giải phương trình sau:
x(x-1)(x-4)(x+5)=84
giúp mk vs ,mấy bn giải chi tiết giúp mk nhé . mk bt kqua rồi nhưng vẫn chưa rõ cách lm ,
Theo dõi (0) 1 Trả lời -


Giải phương trình 2x^3+6x^2=x^3+3x
bởi Mai Thuy
 17/11/2018
17/11/2018
giải pt \(2x^3+6x^2=x^2+3x\)
Theo dõi (0) 1 Trả lời





