Giải bài 28 tr 10 sách BT Toán lớp 8 Tập 2
Giải các phương trình sau:
a. \(\left( {x - 1} \right)\left( {5x + 3} \right) = \left( {3x - 8} \right)\left( {x - 1} \right)\)
b. \(3x\left( {25x + 15} \right) - 35\left( {5x + 3} \right) = 0\)
c. \(\left( {2 - 3x} \right)\left( {x + 11} \right) = \left( {3x - 2} \right)\left( {2 - 5x} \right)\)
d. \(\left( {2{x^2} + 1} \right)\left( {4x - 3} \right) = \left( {2{x^2} + 1} \right)\left( {x - 12} \right)\)
e. \({\left( {2x - 1} \right)^2} + \left( {2 - x} \right)\left( {2x - 1} \right) = 0\)
f. \(\left( {x + 2} \right)\left( {3 - 4x} \right) = {x^2} + 4x + 4\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Chuyển vế phải sang vế trái và phân tích vế trái thành nhân tử.
- Áp dụng phương pháp giải phương trình tích: \(A(x).B(x) = 0 ⇔ A(x) = 0\) hoặc \(B(x) = 0.\)
Lời giải chi tiết
a. \(\left( {x - 1} \right)\left( {5x + 3} \right) = \left( {3x - 8} \right)\left( {x - 1} \right)\)
\(\eqalign{ & \Leftrightarrow \left( {x - 1} \right)\left( {5x + 3} \right) - \left( {3x - 8} \right)\left( {x - 1} \right) = 0 \cr & \Leftrightarrow \left( {x - 1} \right)\left[ {\left( {5x + 3} \right) - \left( {3x - 8} \right)} \right] = 0 \cr & \Leftrightarrow \left( {x - 1} \right)\left( {5x + 3 - 3x + 8} \right) = 0 \cr & \Leftrightarrow \left( {x - 1} \right)\left( {2x + 11} \right) = 0 \cr} \)
\( \Leftrightarrow x - 1 = 0\)hoặc \(2x + 11 = 0\)
+ \(x - 1 = 0 \Leftrightarrow x = 1\)
+ \(2x + 11 = 0 \Leftrightarrow x = - 5,5\)
Phương trình có nghiệm x = 1 hoặc x = -5,5
b. \(3x\left( {25x + 15} \right) - 35\left( {5x + 3} \right) = 0\)
\(\eqalign{ & \Leftrightarrow 15x\left( {5x + 3} \right) - 35\left( {5x + 3} \right) = 0 \cr & \Leftrightarrow \left( {15x - 35} \right)\left( {5x + 3} \right) = 0 \cr} \)
\( \Leftrightarrow 15x - 35 = 0\) hoặc \(5x + 3 = 0\)
+ \(15x - 35 = 0 \Leftrightarrow x = {{35} \over {15}} = {7 \over 3}\)
+ \(5x + 3 = 0 \Leftrightarrow x = - {3 \over 5}\)
Phương trình có nghiệm \(x = {7 \over 3}\) hoặc \(x = - {3 \over 5}\)
c. \(\left( {2 - 3x} \right)\left( {x + 11} \right) = \left( {3x - 2} \right)\left( {2 - 5x} \right)\)
\(\eqalign{ & \Leftrightarrow \left( {2 - 3x} \right)\left( {x + 11} \right) - \left( {3x - 2} \right)\left( {2 - 5x} \right) = 0 \cr & \Leftrightarrow \left( {2 - 3x} \right)\left( {x + 11} \right) + \left( {2 - 3x} \right)\left( {2 - 5x} \right) = 0 \cr & \Leftrightarrow \left( {2 - 3x} \right)\left[ {\left( {x + 11} \right) + \left( {2 - 5x} \right)} \right] = 0 \cr & \Leftrightarrow \left( {2 - 3x} \right)\left( {x + 11 + 2 - 5x} \right) = 0 \cr & \Leftrightarrow \left( {2 - 3x} \right)\left( { - 4x + 13} \right) = 0 \cr} \)
\( \Leftrightarrow 2 - 3x = 0\)hoặc \(13 - 4x = 0\)
+ \(2 - 3x = 0 \Leftrightarrow x = {2 \over 3}\)
+ \(13 - 4x = 0 \Leftrightarrow x = {{13} \over 4}\)
Phương trình có nghiệm \(x = {2 \over 3}\) hoặc \(x = {{13} \over 4}\)
d. \(\left( {2{x^2} + 1} \right)\left( {4x - 3} \right) = \left( {2{x^2} + 1} \right)\left( {x - 12} \right)\)
\(\eqalign{ & \Leftrightarrow \left( {2{x^2} + 1} \right)\left( {4x - 3} \right) - \left( {2{x^2} + 1} \right)\left( {x - 12} \right) = 0 \cr & \Leftrightarrow \left( {2{x^2} + 1} \right)\left[ {\left( {4x - 3} \right) - \left( {x - 12} \right)} \right] = 0 \cr & \Leftrightarrow \left( {2{x^2} + 1} \right)\left( {4x - 3 - x + 12} \right) = 0 \cr & \Leftrightarrow \left( {2{x^2} + 1} \right)\left( {3x + 9} \right) = 0 \cr} \)
\( \Leftrightarrow 2{x^2} + 1 = 0\)hoặc \(3x + 9 = 0\)
+ \(2{x^2} + 1 = 0\) vô nghiệm (\(2{x^2} \ge 0\) nên \(2{x^2} + 1 > 0$ )
+ \(3x + 9 = 0 \Leftrightarrow x = - 3\)
Phương trình có nghiệm x = -3
e. \({\left( {2x - 1} \right)^2} + \left( {2 - x} \right)\left( {2x - 1} \right) = 0\)
\(\eqalign{ & \Leftrightarrow \left( {2x - 1} \right)\left( {2x - 1} \right) + \left( {2 - x} \right)\left( {2x - 1} \right) = 0 \cr & \Leftrightarrow \left( {2x - 1} \right)\left[ {\left( {2x - 1} \right) + \left( {2 - x} \right)} \right] = 0 \cr & \Leftrightarrow \left( {2x - 1} \right)\left( {2x - 1 + 2 - x} \right) = 0 \cr & \Leftrightarrow \left( {2x - 1} \right)\left( {x + 1} \right) = 0 \cr} \)
\( \Leftrightarrow 2x - 1 = 0\)hoặc \(x + 1 = 0\)
+ \(2x - 1 = 0 \Leftrightarrow x = 0,5\)
+ \(x + 1 = 0 \Leftrightarrow x = - 1\)
Phương trình có nghiệm x = 0,5 hoặc x = -1
f. \(\left( {x + 2} \right)\left( {3 - 4x} \right) = {x^2} + 4x + 4\)
\(\eqalign{ & \Leftrightarrow \left( {x + 2} \right)\left( {3 - 4x} \right) - {\left( {x + 2} \right)^2} = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left( {3 - 4x} \right) - \left( {x + 2} \right)\left( {x + 2} \right) = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left[ {\left( {3 - 4x} \right) - \left( {x + 2} \right)} \right] = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left( {3 - 4x - x - 2} \right) = 0 \cr & \Leftrightarrow \left( {x + 2} \right)\left( {1 - 5x} \right) = 0 \cr} \)
\( \Leftrightarrow x + 2 = 0\) hoặc \(1 - 5x = 0\)
+ \(x + 2 = 0 \Leftrightarrow x = - 2\)
+ \(1 - 5x = 0 \Leftrightarrow x = 0,2\)
Phương trình có nghiệm x = -2 hoặc x = 0,2
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Giải phương trình (6x+1)/(x^2-7x+10)+5/(x-2)=3/(x-5)
bởi Trọng Bùi
 25/03/2020
25/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho phân thức 3x^2+6x+12/x^3-8
a tìm điều kiện của x để phân thức đã cho được xác định
B rút gọn phân thức sau khi rút gọn với x= 4001/2000
Theo dõi (0) 4 Trả lời -


Giải phương trình (2x+7)^2=(x+3)^2
bởi Đóm Trần
 24/03/2020
24/03/2020
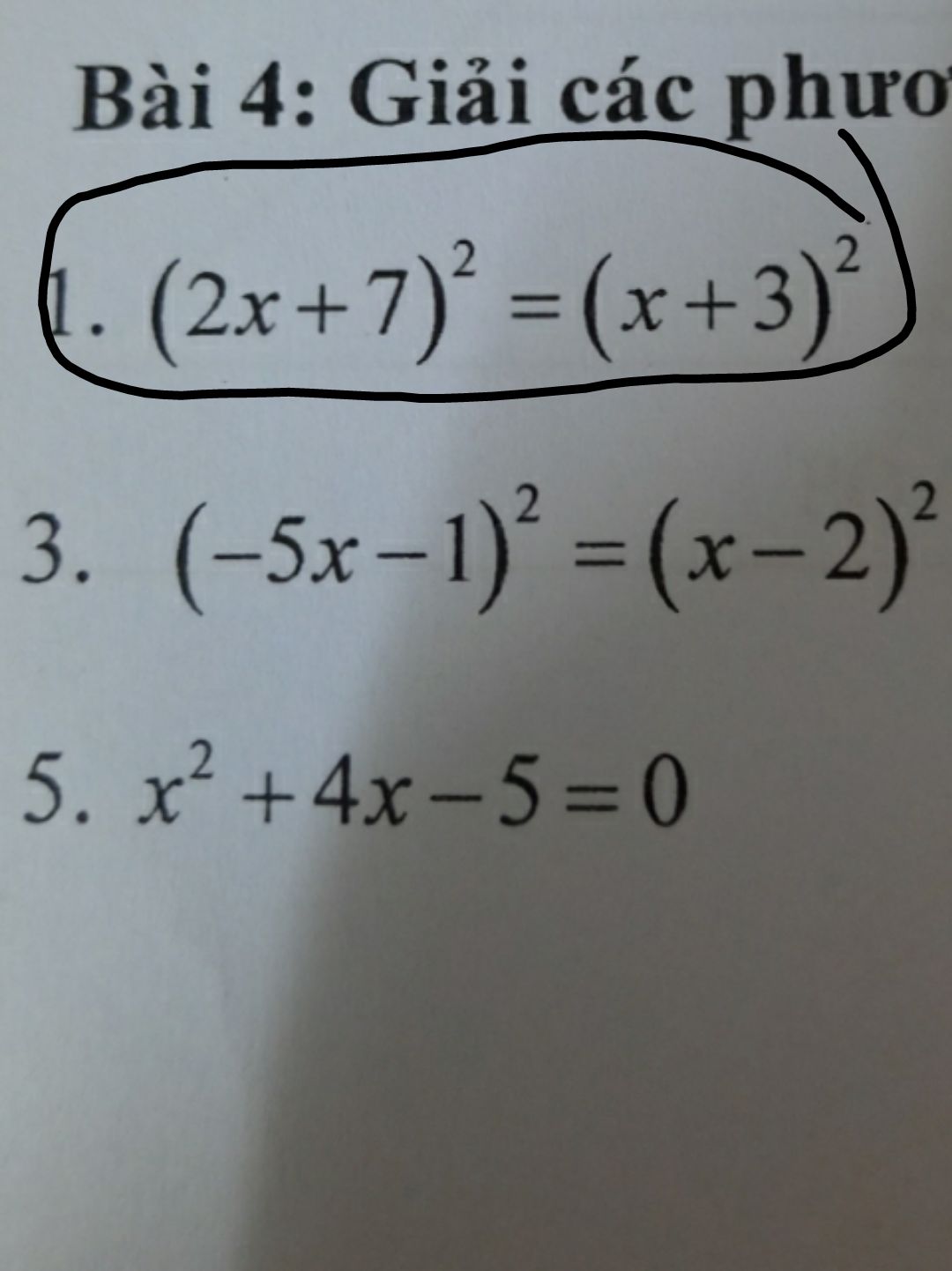 Theo dõi (1) 10 Trả lời
Theo dõi (1) 10 Trả lời -

 Giúp tui vsTheo dõi (0) 1 Trả lời
Giúp tui vsTheo dõi (0) 1 Trả lời -
ADMICRO


Tìm điều kiện của x để biểu thức (3x-1)/(x^2-4) xác định
bởi lin
 23/03/2020
23/03/2020
Tìm điều kiện của x để biểu thức sau là phân thức
Theo dõi (0) 1 Trả lời -


Giải phương trình (x+2)(x-3)=0
bởi Vũ Tiểu
 20/03/2020
20/03/2020
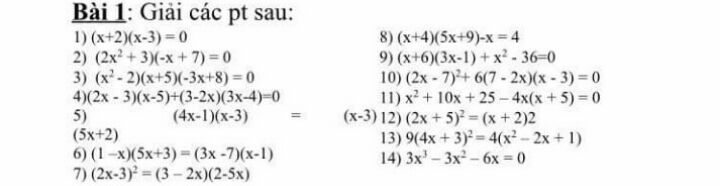 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Giải phương trình (x+1)/(x-2)-5/(x+2)-12/(x^2-4)+1
bởi Phạm Ngân
 20/03/2020
20/03/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Giải phương trình (2x+7)^2=9(x+2)^2
bởi Oanh Lê Kiều
 19/03/2020
Giải Phương trình
19/03/2020
Giải Phương trình Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình (5x-4)(4x+6)=0
bởi Oanh Lê Kiều
 19/03/2020
Giải Phương trình
19/03/2020
Giải Phương trình Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Giải phương trình (3x-2)(4x+5)=0
bởi Nguyễn Đức Trung Kiên
 19/03/2020
19/03/2020
(3x-2)(4x+5)=0
(4x+2)(x2+1)=0
Theo dõi (0) 2 Trả lời -


Thực hiện phép tính ((5x+y)/(x^2-5xy)+(5x-y)/(x^2+5xy)) (x^2-25y^2)/(x^2+y^2 )
bởi Trung Trương
 18/03/2020
Mk ko rõ
18/03/2020
Mk ko rõ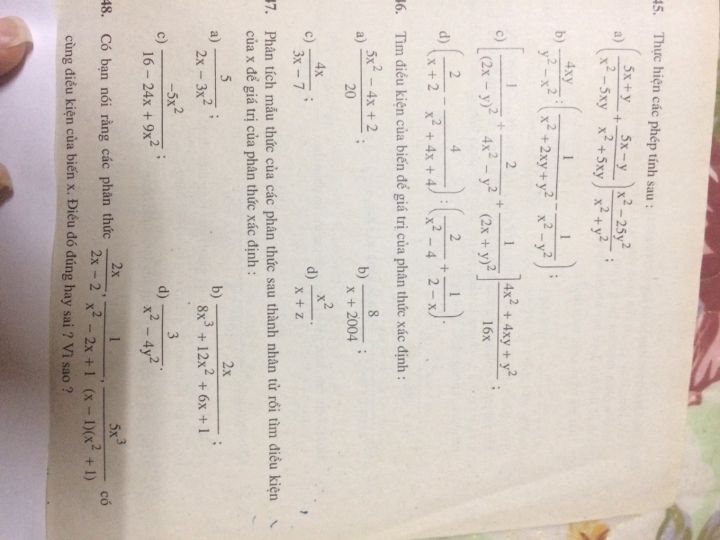 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính số sản phẩm mà tổ sản xuất được giao
bởi Lê Nguyên
 18/03/2020
18/03/2020
Giải bài toán bằng cách lập phương trình : Một tổ sản xuất dự định hoàn thành công việc trong 12 ngày . Thời gian đầu họ làm mỗi ngày 20 sản phẩm . Sau khi làm được 1 nữa số sản phấm đã giao , nhờ hợp lý hóa một số thao tác , mỗi giờ họ làm được 30 sản phẩm nữa so với mỗi ngày trước đó . Tính số sản phẩm mà tổ sản xuất được giao.
Theo dõi (0) 1 Trả lời -


Giải phuorng trình
bởi Phan Lương quyến
 16/03/2020
Giải phương trình
16/03/2020
Giải phương trình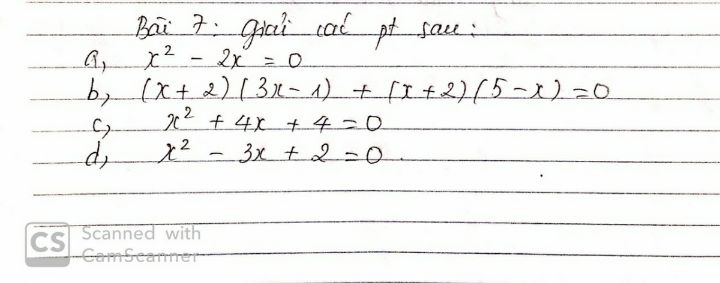 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Ôn tập Giải phương tình
bởi Thanh Chung
 16/03/2020
Ở đây nhé bạn
16/03/2020
Ở đây nhé bạn Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


bởi Thanh Chung
 16/03/2020
Theo dõi (1) 1 Trả lời
16/03/2020
Theo dõi (1) 1 Trả lời -


Giải phương trình 7x-4 =3x+1
bởi Nguyễn Thanh
 13/03/2020
13/03/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Giải phương trình (9x^2-4)(x+1)=(3x+2)(x^2-1)
bởi Tit Mit
 11/03/2020
11/03/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Giải phương trình 2(1-3x)/5 - (2+3x)/10=7-3(2x+1)/4
bởi Út Pham Hoà
 11/03/2020
11/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình 11+8x-3=5x-3+x
bởi oanh Trần
 09/03/2020
09/03/2020
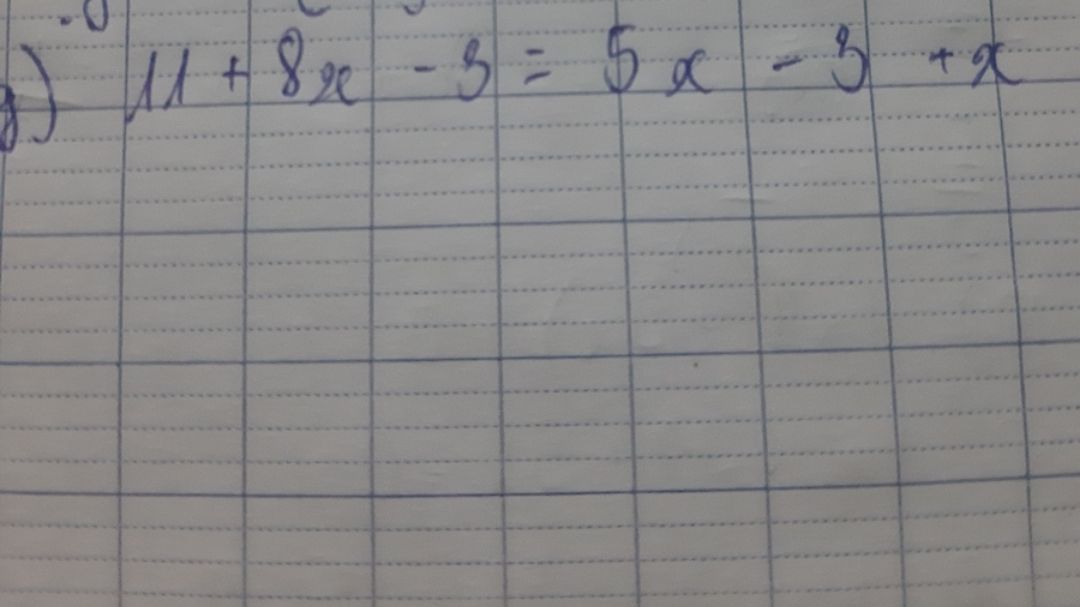 Theo dõi (1) 13 Trả lời
Theo dõi (1) 13 Trả lời -


Giải phương trình (x^2+1)(x^2-4x+4)=0
bởi oanh Trần
 08/03/2020
08/03/2020
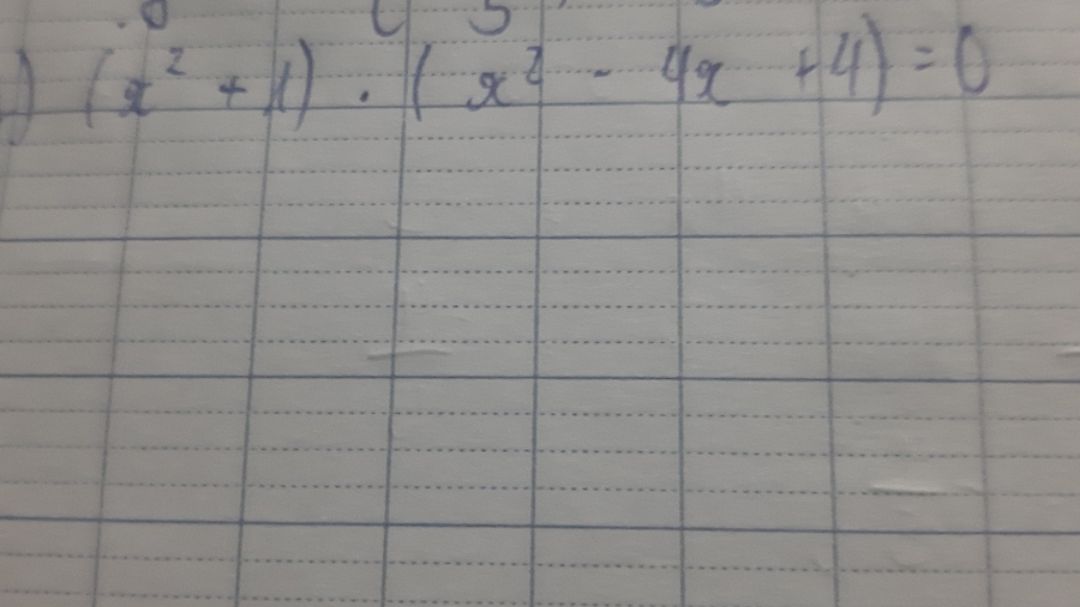 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm m để phương trình b(4m²-9)x=2m² m-3 đã cho có nghiệm duy nhất; vô số nghiệm.
bởi Tú Dương
 06/03/2020
Giúp mình với các bạn mình đang cần gấpTheo dõi (0) 0 Trả lời
06/03/2020
Giúp mình với các bạn mình đang cần gấpTheo dõi (0) 0 Trả lời -


Giải phương trình 5x(x+ 5)=(x+ 5)(3-2x)
bởi Nguyễn Lương
 05/03/2020
05/03/2020
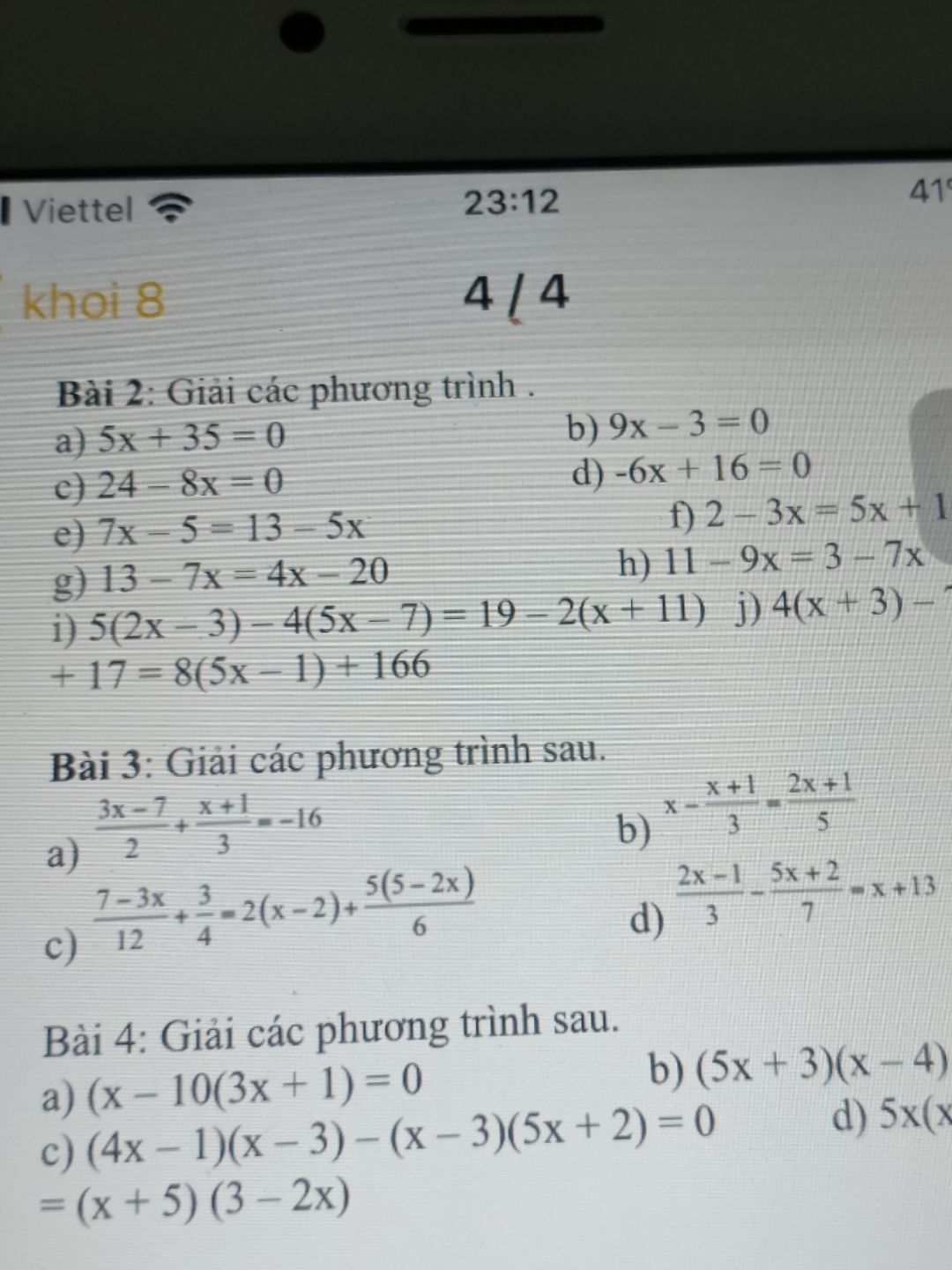 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình 1/(2x-3)-3/x(2x-3)=5/x
bởi Hồng Ánh Hoa
 05/03/2020
05/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (3x 1).(x 2)=(3x 11).(7x-10)
bởi Trai' Họ Mạnh'x
 02/03/2020
Giải phương trìnhTheo dõi (0) 0 Trả lời
02/03/2020
Giải phương trìnhTheo dõi (0) 0 Trả lời -


Tìm x biết 3x^2-7x+1=0
bởi Lan Anh
 29/02/2020
29/02/2020
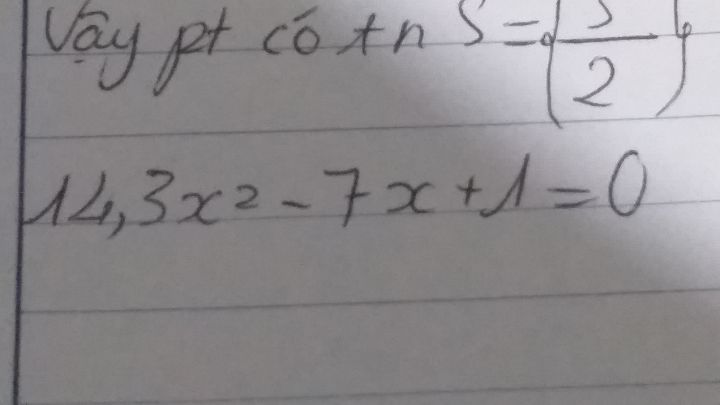 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (x-2)^2-(2x-3)^2=0
bởi Minh Nguyen
 29/02/2020
Tôi muốm giải câu này giúp tôi nhaTheo dõi (2) 3 Trả lời
29/02/2020
Tôi muốm giải câu này giúp tôi nhaTheo dõi (2) 3 Trả lời -


Tìm x biết (x-2)(3x 5)=(2x-4)(x+1)
bởi Linh Vo
 28/02/2020
Giai cac phương trinh sau
28/02/2020
Giai cac phương trinh sau Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình x^2+2x-3=0
bởi Cao Cao phuong uyen
 28/02/2020
28/02/2020
1/x^2+2x-3=0
2/ 2x^3=x^2-2x-1
3/(x-1)(x^2+5x-2)-x^3+1=0
4/x^2+(x+2)(11x-7)=4
5/4x^2-12x+5=0
Theo dõi (0) 2 Trả lời -


Tìm x biết 2x^3=x^2-2x-1
bởi Cao Cao phuong uyen
 28/02/2020
28/02/2020
2x^3=x^2-2x-1
Theo dõi (0) 0 Trả lời -


Tìm x biết x^2-4-2(x+4)=0
bởi Thảoo Bê
 27/02/2020
x^2-4-2(x 4)=0Theo dõi (0) 1 Trả lời
27/02/2020
x^2-4-2(x 4)=0Theo dõi (0) 1 Trả lời -


Giải phương trình 3x - 15 = 2x( x - 5 )
bởi Nguyễn Danh
 24/02/2020
3x - 15 = 2x( x - 5 )Theo dõi (0) 6 Trả lời
24/02/2020
3x - 15 = 2x( x - 5 )Theo dõi (0) 6 Trả lời -


Giải phương trình (5x-3)(4x+7)=0
bởi Yorn Nguyễn
 23/02/2020
Giúp mình vs ạ, đang cần gấp
23/02/2020
Giúp mình vs ạ, đang cần gấp Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình -x^2+5x+6=0
bởi Jun Nguyễn
 22/02/2020
22/02/2020
.
giải phương trình trên
Theo dõi (0) 3 Trả lời -


Tìm x biết (x^2-6x-9)-4=0
bởi Duyên Thị Hoàng
 20/02/2020
Hỏi bài tập
20/02/2020
Hỏi bài tập Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm y biết y(y-1/2)(2y+5)=0
bởi Thanh Truc
 20/02/2020
20/02/2020
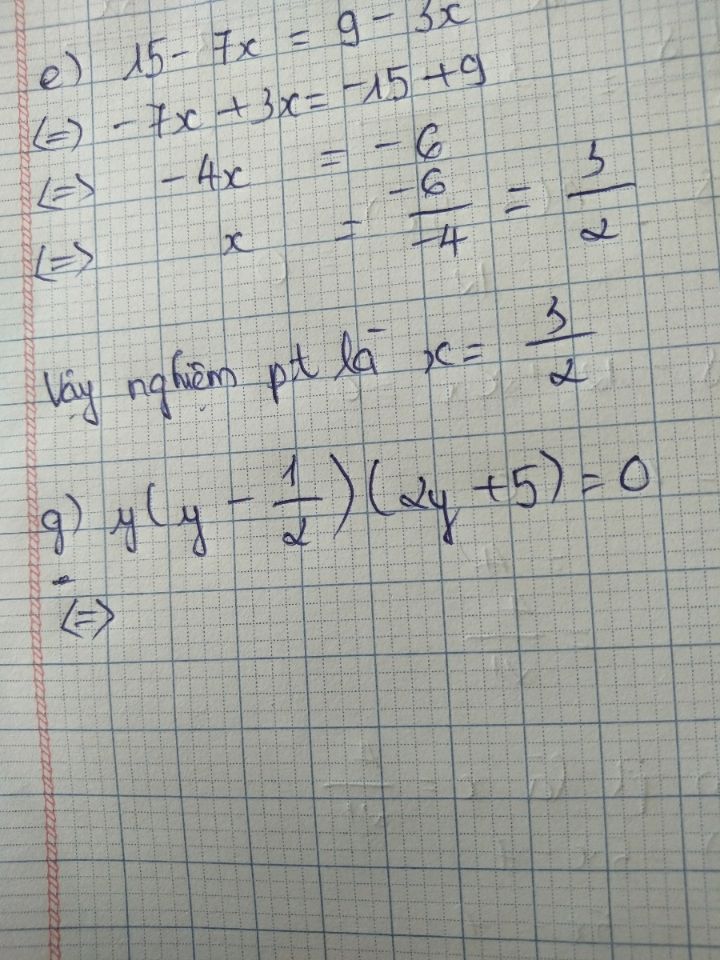 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời



