Giải bài 147 tr 98 sách BT Toán lớp 8 Tập 1
Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Vận dụng dấu hiệu nhận biết của các hình đã học để tìm lời giải cho bài toán.
Tứ giác có 3 góc vuông là hình chữ nhật
Hình chữ nhật có 2 cạnh kề bằng nhau là hình vuông.
Lời giải chi tiết
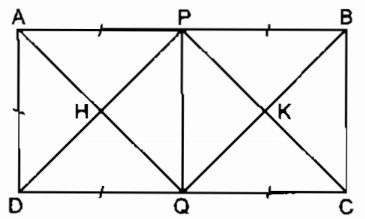
Xét tứ giác APQD ta có:
AB // CD (gt) hay AP // QD
AP = \({1 \over 2}\)AB (gt)
QD = \({1 \over 2}\)CD (gt)
Suy ra: AP = QD nên tứ giác APQD là hình bình hành.
\(\widehat A = {90^0}\)
Suy ra: Tứ giác APQD là hình chữ nhật
AD = AP = \({1 \over 2}\)AB
Vậy : Tứ giác APQD là hình vuông
⇒ AQ ⊥ PD (tính chất hình vuông) \( \Rightarrow \widehat {PHQ} = {90^0}\) (1)
HP = HQ (tính chất hình vuông)
- Xét tứ giác PBCQ ta có:
PB // CD
PB = \({1 \over 2}\)AB (gt)
CQ = \({1 \over 2}\)CD (gt)
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
\(\widehat B = {90^0}\)suy ra tứ giác PBCQ là hình chữ nhật
PB = BC (vì cùng bằng AD = \({1 \over 2}\)AB)
Vậy: Tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (tính chất hình vuông) \( \Rightarrow \widehat {PKQ} = {90^0}\)(2)
PD là tia phân giác \(\widehat {APQ}\) (tính chất hình vuông)
PC là tia phân giác \(\widehat {QPB}\) (tính chất hình vuông)
Suy ra: PD ⊥ PC (tính chất hai góc kề bù) ⇒ \(\widehat {HPK} = {90^0}\) (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 145 trang 98 SBT Toán 8 Tập 1
Bài tập 146 trang 98 SBT Toán 8 Tập 1
Bài tập 148 trang 98 SBT Toán 8 Tập 1
Bài tập 149 trang 98 SBT Toán 8 Tập 1
Bài tập 150 trang 98 SBT Toán 8 Tập 1
Bài tập 151 trang 98 SBT Toán 8 Tập 1
Bài tập 152 trang 99 SBT Toán 8 Tập 1
Bài tập 153 trang 99 SBT Toán 8 Tập 1
Bài tập 154 trang 99 SBT Toán 8 Tập 1
Bài tập 155 trang 99 SBT Toán 8 Tập 1
Bài tập 156 trang 99 SBT Toán 8 Tập 1
Bài tập 12.1 trang 99 SBT Toán 8 Tập 1
-


Câu hỏi: Cho tam giác ABC (AB>AC). Trên đoạn AB lấy điểm E sao cho BE = AC. Gọi P, Q lần lượt là trung điểm các cạnh AB và CE. AM là tia phân giác góc BAC ( M € BC ) . Chứng minh rằng: AM vuông góc với PQ.
Please help me.
Theo dõi (1) 1 Trả lời -


Chứng minh BJ và DE vuông góc biết I nằm trên AB, E là giao điểm của DI và CB
bởi Nguyễn Hoàng Ngân
 14/09/2018
14/09/2018
Cho hình vuông ABCD. I nằm trên AB. E là giao điểm của Di và CB. J là giao điểm của AE và CI. Chứng minh BJ và DE vuông góc với nhau.
Theo dõi (0) 1 Trả lời -


Tính đườnh chéo của hình vuông cạnh bằng 1
bởi Nguyễn Thị Trang
 31/05/2019
31/05/2019
Một hình vuông cạnh bằng 1 thì độ dài đường chéo là bao nhiêu ?
Giúp mình với !
Theo dõi (0) 1 Trả lời -


Bài 1
Cho tam giác ABC vuông cân tại A có AD là đường trung tuyến. Qua D kẻ DE vuông góc với AB tại E và DF vuông góc với AC tại F
a)Tứ giác AEDF là hình gì? Vì sao?
b) Biết BC = 20cm. Tính AD?
Bài 2
Cho hình thang ABCD vuông góc tại A . Đáy AD=2BC, đường chéo AC là phân giác A . Vẽ CE song song AB . Chứng minh
a. ABCE là hình vuông
b.BCDE là hình bình hành
c. Tam giác CAD vuông cân
Bài 3
Cho tam giác ABC cân tại A , đường trung tuyến AM. Gọi I là trung điểm AC, K là điểm đối xứng với M qua I
a. Tứ giác AMCK là hình gì? Vì sao?
b. Tứ giác AKMB là hình gì vì sao
c. tam giác ABC cần thêm điều kiện gì để tứ giác AMCK là hình vuông
Theo dõi (0) 2 Trả lời






