Bài tập 150 trang 98 SBT Toán 8 Tập 1

Hướng dẫn giải

Vận dụng kiến thức : Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Lời giải chi tiết

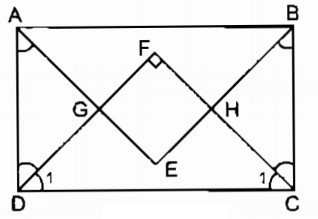
Gọi giao điểm các đường phân giác của các góc: \(widehat A,\widehat B,\widehat C,\widehat D\)theo thứ tự cắt nhau tại E, H, F, G.

Trong ∆ ADG ta có: \(\widehat {GAD} = {45^0};\widehat {GDA} = {45^0}\) (gt)

⇒ ∆ GAD vuông cân tại G

\( \Rightarrow \widehat {AGD} = {90^0}\)và GD = GA

\( \Rightarrow \widehat {FGE} = \widehat {AGD} = {90^0}\)

Trong ∆ BHC ta có:

\(\widehat {HBC} = {45^0};\widehat {HCB} = {45^0}\) (gt)

⇒ ∆HBC vuông cân tại H

\( \Rightarrow \widehat {BHC} = {90^0}\)  và HB = HC

Trong ∆ FDC ta có: \({\widehat D_1} = {45^0};{\widehat C_1} = {45^0}\) (gt)

⇒ ∆ FDC vuông cân tại F \( \Rightarrow \widehat F = {90^0}\) và FD = FC

nên tứ giác EHFG là hình chữ nhật (vì có ba góc vuông)

Xét ∆ GAD và ∆ HBC :

\(\widehat {GAD} = \widehat {HBC} = {45^0}\)

AD = BC (tính chất hình chữ nhật)

\(\widehat {GDA} = \widehat {HCB} = {45^0}\)

Do đó: ∆ GAD = ∆ HBC (g.c.g) ⇒ GD = HC

FD = FC (chứng minh trên)

Suy ra: FG = FH

Vậy hình vuông EHFG có hai cạnh kề bằng nhau nên là hình vuông.

-- Mod Toán 8 HỌC247