Bài tập 125 trang 95 SBT Toán 8 Tập 1

Hướng dẫn giải

Ta sử dụng kiến thức:

+)  Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.

+) Các điểm cách đường thẳng \(b\) một khoảng bằng \(h\) nằm trên hai đường thẳng song song với \(b\) và cách \(b\) một khoảng bằng \(h.\)

Lời giải chi tiết

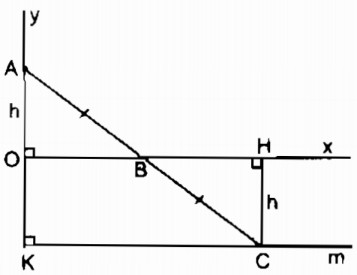
Vì điểm C đối xứng với điểm A qua điểm B ⇒ BA = BC

Kẻ CH ⊥ Ox

Xét hai tam giác vuông AOB và CHB:

\(\widehat {AOB} = \widehat {CHB} = {90^0}\)

BA = BC (chứng minh trên)

\(\widehat {ABO} = \widehat {CBH}\) (đối đỉnh)

Do đó: ∆ AOB = ∆ CHB (cạnh huyền, góc nhọn) ⇒ CH = AO

A, O cố định ⇒ OA không đổi nên CH không đổi.

C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng OA.

Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.

Vậy C chuyển động trên tia Km // Ox, cách Ox một khoảng không đổi bằng OA.

-- Mod Toán 8 HỌC247