Giải bài 127 tr 96 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.
a. So sánh các độ dài AM, DE.
b. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Tứ giác có ba góc vuông là hình chữ nhật.
+) Trong hình chữ nhật, hai đường chéo bằng nhau.
+) Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Lời giải chi tiết
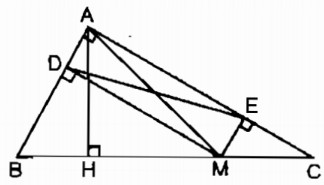
a. Xét tứ giác ADME ta có:
\(\widehat A = {90^0}\) (gt)
MD ⊥ AB (gt)
\( \Rightarrow \widehat {MDA} = {90^0}\)
ME ⊥ AC (gt)
\( \Rightarrow \widehat {MEA} = {90^0}\)
Suy ra: Tứ giác ADME là hình chữ nhật (vì có ba góc vuông)
⇒ AM = DE (tính chất hình chữ nhật)
b. Ta có: AH ⊥ BC nên AM ≥ AH. Dấu “=” xảy ra khi M trùng với H.
mà DE = AM (chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 125 trang 95 SBT Toán 8 Tập 1
Bài tập 126 trang 96 SBT Toán 8 Tập 1
Bài tập 128 trang 96 SBT Toán 8 Tập 1
Bài tập 129 trang 96 SBT Toán 8 Tập 1
Bài tập 130 trang 96 SBT Toán 8 Tập 1
Bài tập 131 trang 96 SBT Toán 8 Tập 1
Bài tập 10.1 trang 96 SBT Toán 8 Tập 1
-


Bài 129* trang 96 sách bài tập toán 8 tập 1
bởi Lê Nhi
 29/09/2018
Bài 129* (Sách bài tập - trang 96)
29/09/2018
Bài 129* (Sách bài tập - trang 96)Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ?
Theo dõi (0) 1 Trả lời -


Bài 127 trang 96 sách bài tập toán 8 tập 1
bởi thu hảo
 29/09/2018
Bài 127 (Sách bài tập - trang 96)
29/09/2018
Bài 127 (Sách bài tập - trang 96)Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC
a) So sánh các độ dài AM, DE
b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất
Theo dõi (0) 1 Trả lời





