Giải bài 53 tr 46 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC\) vuông tại \(A.\) Các tia phân giác của các góc \(B\) và \(C\) cắt nhau tại \(I.\) Gọi \(D\) và \(E\) là chân các đường vuông góc kẻ từ \(I\) đến \(AB\) và \(AC.\)
a) Chứng minh rằng \(AD = AE.\)
b) Tính các độ dài \(AD, AE\) biết rằng \(AB = 6cm, AC = 8cm.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Tính chất đường phân giác của góc: Các điểm nằm trên đường phân giác của một góc cách đều hai cạnh của góc đó.
+) Ba đường phân giác trong tam giác cắt nhau tại một điểm.
+) Tính chất hai tam giác bằng nhau
Lời giải chi tiết
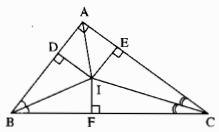
a) I là giao điểm phân giác trong của \(\widehat B\) và \(\widehat C\) nên AI là tia phân giác của Â.
\( \Rightarrow \) ID = IE (tính chất tia phân giác) (1)
∆ADI vuông tại D có \(\widehat {DAI} = 45^\circ \)
Nên ∆ADI vuông cân tại D.
\( \Rightarrow \) ID = DA (2)
∆AEI vuông tại E có \(\widehat {E{\rm{A}}I} = 45^\circ \)
Nên ∆ AEI vuông cân tại E
\( \Rightarrow \) IE = AE (3)
Từ (1), (2) và (3) suy ra: AD = AE
b) Trong tam giác vuông ABC có Â=90°
Theo định lý Pitago ta có:
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& B{C^2} = {6^2} + {8^2} = 36 + 64 = 100 \cr} \)
\( \Rightarrow \) BC = 10 (cm)
Kẻ \(IF \bot BC\)
Xét hai tam giác vuông IDB và IFB:
\(\eqalign{
& \widehat {IDB} = \widehat {IFB} = 90^\circ \cr
& \widehat {DBI} = \widehat {FBI}\left( {gt} \right) \cr} \)
Cạnh huyền BI chung
Do đó: ∆IDB = ∆IFB (cạnh huyền, góc nhọn)
\( \Rightarrow \) DB = FB (4)
Xét hai tam giác vuông IEC và IFC:
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
Cạnh huyền CI chung
Do đó: ∆IEC = ∆IFC (cạnh huyền, góc nhọn)
\( \Rightarrow \) CE = CF (5)
AD + AE = AB – DB + AC – CE
\( \Rightarrow \) AD + AE = AB + AC – (DB + CF) (6)
Từ (4), (5) và (6) suy ra:
AD + AE = AB + AC – (FB + FC) = AB + AC – BC
AD + AE = 6 + 8 – 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
\( \Rightarrow \) AD = AE = 4: 2 = 2 (cm)
-- Mod Toán 7 HỌC247
-


Cho tam giác ABC vuông tại A , phân giác BM và phân giác CN cắt nhau tại K
a, Chứng minh rằng: K cách đều AB và AC
b, Tính số đo góc BKC ?
Theo dõi (0) 1 Trả lời -


Chứng minh góc ESC = (góc ABD + góc ADE) : 2 biết các tia phân giác của các góc ACB và AED cắt nhau ở S
bởi Lê Thánh Tông
 19/12/2019
19/12/2019
cho tam giác ABC. Trên tia đối của tia AB lấy E, trên tia đối của tia AC lấy D. Các tia phân giác của các góc ACB và AED cắt nhau ở S. CMR: góc ESC = ( góc ABD + góc ADE) : 2
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC ( AB = AC ) . Tia phân giác của góc B và C cắt cạnh AC , AB lần lượt ở D và E . Chứng minh rằng :
a) Tam giác AED cân
b) DE // BC
c) DE = BE = DC
Theo dõi (0) 1 Trả lời -


Nêu cách vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau
bởi Thuy Kim
 19/12/2019
19/12/2019
Nêu cách vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau.Vẽ hình minh họa
HELP ME!
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho\(\Delta ABC\) \(\perp A\) ,Trên BC lấy D sao cho BD=BA.Qua D \(\perp BC\) cắt AC tại E. Cắt tia BE tại E
a) c/m \(\Delta BAE=\Delta BDE\)
b) Kẻ AH\(\perp BC\) .c/m AD là tia phân giác
c) Kẻ DK\(\perp AC\) .C/M AH=AK
d) c/m BE \(\perp FC\)
e) c/m AB+AC\(\le BC+AH\)
Theo dõi (0) 1 Trả lời -


Cho tam giác vuông ABC, F là giao điểm của BD và CE, I là giao điểm của ba đường phân giác
bởi thúy ngọc
 28/03/2018
28/03/2018
Giải em bài này với ạ
Cho tam giác vuông ABC \((\widehat A = {90^0})\). Trên cạnh AC Ịấy điểm D sao cho \(\widehat {ABC} = 3\widehat {ABD}\). Trên cạnh AB lấy điểm E sao cho \(\widehat {ACB} = 3\widehat {ACE}\). Gọi F là giao điểm của BD và CE; I là giao điểm của ba đường phân giác của tam giác BFC.
a. Tính \(\widehat {BFC}\).
b. Chứng tỏ rằng tam giác DEI là tam giác đều.
Theo dõi (0) 2 Trả lời -


M.n ơi giải giúp mình câu này vs
Cho tam giác ABC. Gọi I là giao điểm của hai tia phân giác hai góc A và B. Qua I vẽ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Chứng minh rằng: MN = BM + CN.
Theo dõi (0) 2 Trả lời -


Cho tam giác ABC hai đường pgiac trong của hai góc B và C, cmr ba điểm A, I, D thẳng hàng
bởi thu hảo
 28/03/2018
28/03/2018
Ad ơi, giải giúp em với
Cho tam giác ABC hai đường phân giác trong của hai góc \(\widehat B\) và \( \widehat C\) cắt nhau ở điểm I và hai đường phân giác ngoài của hai góc ấy cắt nhau ở điểm D. Chứng minh rằng ba điểm A, I, D thẳng hàng.
Theo dõi (0) 2 Trả lời -


bạn nào biết giải giúp với
Hai đường phân giác của góc B và C trong tam giác ABC cắt nhau ở I. Chứng minh rằng: \(\widehat {BIC} = 90 + \frac{{\widehat A}}{2}\)
Theo dõi (0) 2 Trả lời -


ai giải giúp bài toan này với
bởi Phạm Thiện
 13/08/2017
13/08/2017
cho ta giac abc có góc a là 120 độ,ad là tia phân giác,tia phân giác góc ngoài tại c cắt ab tại k, dk cắt ac tại e.tính góc bed
Theo dõi (0) 2 Trả lời





