Nội dung bài học sẽ giới thiệu đến các em khái niệm và tính chất của Hai góc đối đỉnh cùng với những dạng bài tập liên quan. Bên cạnh đó là những bài tập có hướng dẫn giải chi tiết sẽ giúp các em nắm được phương pháp giải các bài toán liên quan đề hai góc đối đỉnh.
Tóm tắt lý thuyết
1.1. Định nghĩa
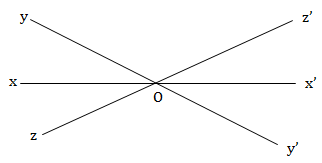
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của mỗi cạnh góc kia.
.png)
1.2. Tính chất
Hai góc đối đỉnh thì bằng nhau \(\widehat {xOy}\) đối đỉnh \(\widehat {x'Oy'} \Rightarrow \widehat {xOy} = \widehat {x'Oy'}\).
Ví dụ 1:
Cho hai đường thẳng xy và zt cắt nhau tại O. Biết góc \(\widehat {xOt}\) lớn gấp 4 lần góc \(\widehat {xOz}\). Tính các góc \(\widehat {xOt},\widehat {tOy},\widehat {xOz}\) và \(\widehat {xOz}.\)
Hướng dẫn giải:
.png)
Ta có góc \(\widehat {xOt}\) và \(\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOt} + \widehat {xOz} = {180^0}\) mà \(\widehat {xOt} = 4\widehat {xOz}\)
Do đó \(4\widehat {xOt} + \widehat {xOz} = {180^0}\,\,\,\,hay\,\,\,\,5\,\,\widehat {xOz}\, = {180^0}\)
Vậy \(\widehat {xOz} = {180^0}:5 = {36^0}\)
Suy ra \(\widehat {xOt} = {4.36^0} = {144^0}\)
Các cặp góc \(\widehat {yOz}\) và \(\widehat {xOt},\,\,\widehat {tOy}\) và \(\widehat {xOz}\) là các cặp góc đổi đỉnh do đó:
\(\begin{array}{l}\widehat {yOz} = \widehat {xOt} = {144^0}\\\widehat {tOy} = \widehat {xOz} = {36^0}\end{array}\)
Ví dụ 2:
Xem các hình a, b, c, d:
.png)
Hỏi cặp góc nào đối đỉnh, cặp góc nào không đối đỉnh? Vì sao?
Hướng dẫn giải:
a. Hai góc này không đối đỉnh vì chúng không có đỉnh chung.
b. Hai góc này không đối đỉnh vì mỗi cạnh của góc này không là tia đối của một cạnh của góc kia.
c. Hai góc đối đỉnh vì mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
d. Hai góc này không đối đỉnh vì một cạnh của góc này không là tia đối của cạnh góc kia.
Ví dụ 3:
Ta có: Hai góc không có điểm trong chung là hai góc mà mỗi cạnh góc này không nằm giữa hai cạnh góc kia.
.png)
Cho ba đường thẳng phân biệt x’x, y’y, z’z cắt nhau ở điểm O.
a. Hãy tìm 6 cặp góc đối đỉnh.
b. Có bao nhiêu cặp góc đối đỉnh không có điểm trong chung?
Hướng dẫn giải:
a. Có 6 cặp góc đối đỉnh là: \(\widehat {x'Oy'}\) và \(\widehat {xOy\,},\,\widehat {y'Oz'}\) và \(\widehat {yOz},\,\widehat {x'Oz'}\) và \(\widehat {zOx\,},\,\widehat {xOy}\) và \(\widehat {xOy'},\widehat {y'Oz}\) và \(\widehat {yOz'},\widehat {z'Ox}\) và \(\widehat {zOx'}.\)
b. Có ba cặp góc đối đỉnh không có điểm chung trong là: \(\widehat {x'Oy'}\) và \(\widehat {xOy},\widehat {y'Oz}\) và \(\widehat {yOz'},\widehat {z'Ox'}\) và \(\widehat {zOx}.\)
Bài tập minh họa
Bài 1:
Cho \(\widehat {xOy} = {100^0}\) và hai góc \(\widehat {yOz}\) và \(\widehat {xOt}\) cùng kề bù với nó. Hãy xác định hai cặp đối đỉnh và tính số đo của các góc \(\widehat {zOt}\), \(\widehat {xOt}\), \(\widehat {yOz}\).
Hướng dẫn giải:
.png)
- Ta có \(\widehat {xOt}\) kề bù với \(\widehat {xOy}\) nên 2 tia Oy, Ot đối nhau.
\(\widehat {yOz}\) kề bù với \(\widehat {xOy}\) nên 2 tia Ox, Oz đối nhau.
Vậy ta được hai cặp góc đối đỉnh là \(\widehat {xOy}\) và \(\widehat {zOt}\); \(\widehat {xOt}\) và \(\widehat {zOy}\).
- Ta có \(\widehat {xOy} = \widehat {zOt} = {100^0}\) (đối đỉnh) và \(\widehat {xOy} + \widehat {yOz} = {180^0}\) (kề bù)
Hay \({100^0} + \widehat {yOz} = {180^0}\)
Suy ra \(\widehat {yOz} = {180^0} - {100^0} = {80^0}\)
Nên \(\widehat {yOz} = \widehat {tOx} = {80^0}\) đối đỉnh
Bài 2:
Cho hai đường thẳng x’x và y’y cắt nhau tại O.
a. Hỏi hai đường thẳng cắt nhau đó tạo thành mấy góc (khác góc bẹt)
b. Tính số đo mỗi góc tạo thành. Nếu biết hiệu số đo của hai góc kề bù là \({30^0}.\)
Hướng dẫn giải:
a. Hai đường thẳng cắt nhau tạo thành 4 góc bẹt: \(xOy,\,\,yOx',\,\,x'Oy'\) và \(y'Ox.\)
b.
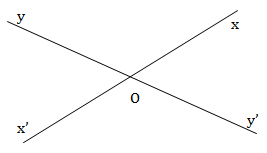
Gọi \(\widehat {xOy}\) và \(\widehat {yOx'}\) là hai góc kề bù.
Giả sử \(\widehat {xOy} - \widehat {yOx'} = {30^0}\)
Lại có \(\widehat {xOy} + \widehat {yOx'} = {180^0}\) (do hai góc kề bù)
\(\begin{array}{l} \Rightarrow 2x\widehat {Oy} = {210^0} \Rightarrow \widehat {xOy} = {150^0}\\ \Rightarrow \widehat {yOx'} = {180^0} - {150^0} = {75^0}\\ \Rightarrow \widehat {xOy'} = \widehat {yOx'} = {75^0}\end{array}\)
Và \(\widehat {x'Oy'} = \widehat {xOy} = {105^0}\) (hai góc đối đỉnh).
Bài 3:
Cho góc bẹt \(\widehat {AOB}\). Trên cùng một nửa mặt phẳng bờ AB, ta vẽ hai tia OC và OD sao cho \(\widehat {AOC} = \widehat {BOD} = {30^0}\)
a. Hai góc \(\widehat {AOC}\) và \(\widehat {BOD}\) có phải là hai góc đối đỉnh không?
b. Vẽ tia OE sao cho tia OB là tia phân giác của góc \(\widehat {DOE}\). Hai góc \(\widehat {AOC}\) và \(\widehat {BOE}\) có phải là hai góc đối đỉnh không?
Hướng dẫn giải:
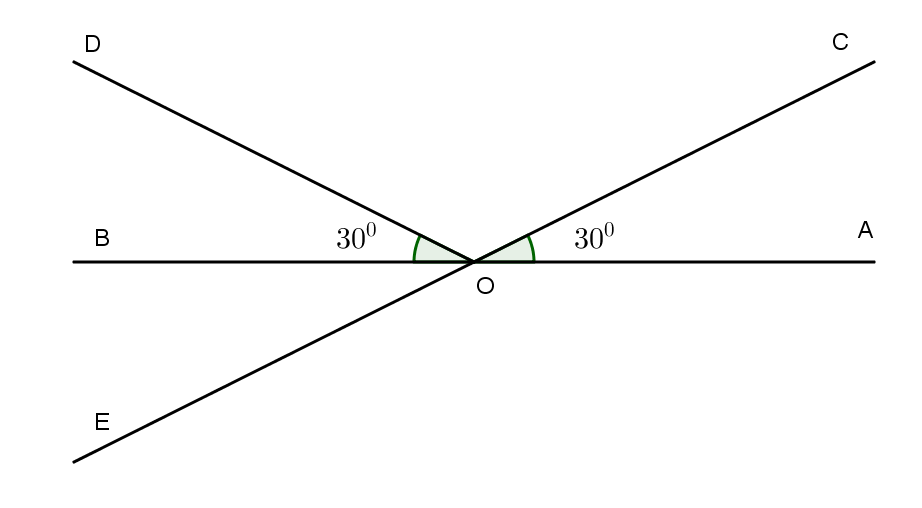
a. Hai góc \(\widehat {AOC}\) và \(\widehat {BOD}\) có một cặp cạnh là hai tia đối nhau, cặp cạnh còn lại không đối nhau nên góc đó không phải là hai góc đối đỉnh.
b. Ta có \(\widehat {AOC} = {30^0}\) nên \(\widehat {BOC} = {150^0}\) (tính chất hai góc kề bù).
Tia OB là tia phân giác của góc \(\widehat {DOE}\) nên \(\widehat {BOD} = \widehat {BOE} = {30^0}\) và tia OD, OE thuộc hai nửa mặt phẳng đối nhau bờ AB.
Suy ra hai tia OC và OE thuộc hai nửa mặt phẳng đối nhau bờ chứa tia OB.
Ta có \(\widehat {BOC} + \widehat {BOE} = {150^0} + {30^0} = {180^0}\)
Suy ra hai tia OC, OE đối nhau.
Hai góc \(\widehat {AOC}\) và \(\widehat {BOE}\) có hai cặp cạnh là hai tia đối nhau nên chúng là hai góc đối đỉnh.
3. Luyện tập Bài 1 Chương 1 Hình học 7
Qua bài giảng Hai góc đối đỉnh này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Định nghĩa và tính chất hai góc đối đỉnh
3.1. Trắc nghiệm về Hai góc đối đỉnh
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 7 Bài 1 cực hay có đáp án và lời giải chi tiết.
-
- A. 1 cạnh của góc này là tia đối của 1 cạnh của góc
- B. mỗi cạnh của góc này là tia đối của 1 cạnh của góc kia
- C. tổng của hai góc bằng 1800
- D. Số đo của chúng bằng nhau
-
Câu 2:
Hai góc đối đỉnh thì:
- A. bằng nhau
- B. bù nhau
- C. kề, bù nhau
- D. cả 3 câu trên đều sai
-
- A. hai góc đồng vị bằng nhau
- B. hai góc trong cùng phía bù nhau
- C. hai góc so le trong bằng nhau
- D. cả 3 câu trên đêu sai
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK về Hai góc đối đỉnh
Các em có thể xem thêm phần hướng dẫn Giải bài tập Hình học 7 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 1 trang 82 SGK Toán 7 Tập 1
Bài tập 2 trang 82 SGK Toán 7 Tập 1
Bài tập 3 trang 82 SGK Toán 7 Tập 1
Bài tập 4 trang 82 SGK Toán 7 Tập 1
Bài tập 5 trang 82 SGK Toán 7 Tập 1
Bài tập 6 trang 83 SGK Toán 7 Tập 1
Bài tập 7 trang 83 SGK Toán 7 Tập 1
Bài tập 8 trang 83 SGK Toán 7 Tập 1
Bài tập 9 trang 83 SGK Toán 7 Tập 1
Bài tập 10 trang 83 SGK Toán 7 Tập 1
Bài tập 1 trang 99 SBT Toán 7 Tập 1
Bài tập 2 trang 99 SBT Toán 7 Tập 1
Bài tập 3 trang 100 SBT Toán 7 Tập 1
Bài tập 4 trang 100 SBT Toán 7 Tập 1
Bài tập 5 trang 100 SBT Toán 7 Tập 1
Bài tập 6 trang 100 SBT Toán 7 Tập 1
Bài tập 7 trang 100 SBT Toán 7 Tập 1
Bài tập 1.1 trang 100 SBT Toán 7 Tập 1
Bài tập 1.2 trang 101 SBT Toán 7 Tập 1
Bài tập 1.3 trang 101 SBT Toán 7 Tập 1
Bài tập 1.4 trang 101 SBT Toán 7 Tập 1
4. Hỏi đáp Bài 1 Chương 1 Hình học 7
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 7 HỌC247











