Giải bài 1.2 tr 101 sách BT Toán lớp 7 Tập 1
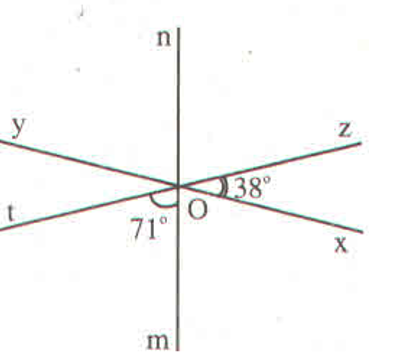
Ba đường thẳng phân biệt \(xy, mn, zt\) cùng đi qua điểm \(O\) và tạo thành các góc \(\widehat {zOx} = {38^o},\,\widehat {tOm} = {71^o}\) (h.bs 1).
a) Đọc tên các cặp góc đối đỉnh có trong hình đó.
b) Cho biết số đo của các góc còn lại có trong hình đó.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Tính chất: Hai góc đối đỉnh thì bằng nhau.
- Tổng hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
a) Các cặp góc đối đỉnh là: \(\widehat {xOz}\) và \(\widehat {tOy}\); \(\widehat {xOn}\) và \(\widehat {mOy}\); \(\widehat {zOn}\) và \(\widehat {tOm}\); \(\widehat {xOm}\) và \(\widehat {nOy}\); \(\widehat {xOt}\) và \(\widehat {zOy}\), \(\widehat {mOz}\) và \(\widehat {tOn}\); các góc bẹt như \(tOz, yOx, nOm\) có góc đối đỉnh là chính nó.
b) Từ các cặp góc đối đỉnh suy ra ngay:
\(\widehat {zOx} = \widehat {tOy} = 38^\circ ,\widehat {tOm} = \widehat {zOn} = 71^\circ \)
\(\widehat {tOz}\) là góc bẹt nên ta có:
\(\begin{array}{l}
\widehat {tOm} + \widehat {mOx} + \widehat {xOz} = {180^0}\\
\Rightarrow \widehat {xOm} = {180^0} - \left( {\widehat {tOm} + \widehat {xOz}} \right)
\end{array}\)
\(\Rightarrow \widehat {xOm} = 180^\circ - \left( {71^\circ + 38^\circ } \right) = 71^\circ \)
Từ đó, \(\widehat {xOm} = \widehat {yOn} = 71^\circ \).
Các góc bẹt như \(tOz, yOx, nOm\) đều có số đo là \(180^\circ \)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
-
Cho tam giác ABC vuông tại A có AB=9cm; AC=12cm.
a) tính BC
b) Tia phân giác của góc B cắt Ac tại D. Kẻ DM vuông góc với BC tịa M . chứng minh tam giác ABD=MBD
c)Gọi giao điểm của DM và AB là E . Chứng minh tam giác BEC cân .
d) Kẻ BD cắt EC tại K . GỌI P;Q lần lượt là trung diểm của Bc và BE biết rằng BK cắt EP tại I . chứng minh C:I:Q thẳng hàng
Theo dõi (0) 1 Trả lời -
Chứng minh ít nhất có hai đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 20 độ
bởi Lê Viết Khánh
26/04/2019
Cho 9 đường thẳng trong đó không có 2 đường thẳng nào song song. Chứng minh rằng ít nhất cũng có hai đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 20 độ
Theo dõi (0) 1 Trả lời -
Có bao nhiêu cặp góc đối đỉnh nhỏ hơn góc bẹt khi vẽ 16 đường thẳng qua điểm O ?
bởi minh vương
08/05/2019
Qua điểm O vẽ 16 đường thẳng đôi một phân biệt. Hỏi có bao nhêu cặp góc đối đỉnh nhỏ hơn góc bẹt?
Theo dõi (0) 1 Trả lời -
Viết tên hai góc vuông không đối đỉnh khi vẽ góc xAy và x'Ay' đối đỉnh với góc xAy
bởi Quế Anh
19/09/2018
Luyện tập - Bài 9 (SGK tập 1 trang 83)Vẽ góc xAy. Vẽ góc x'Ay' đối đỉnh với góc xAy. Hãy viết tên hai góc vuông không đối đỉnh ?
Theo dõi (0) 1 Trả lời -
ADMICRO
Viết tên hai cặp góc đối đỉnh khi vẽ hai đường thẳng zz' và tt' cắt nhau tại A
bởi Dương Quá
19/09/2018
Bài 3 (SGK tập 1 trang 82)Vẽ hai đường thẳng zz' và tt' cắt nhau tại A. Hãy viết tên hai cặp góc đối đỉnh ?
Theo dõi (0) 1 Trả lời -
Bài 1 trang 82 sách giáo khoa toán 7 tập 1
bởi Ngoc Nga
19/09/2018
Bài 1 (SGK tập 1 trang 82)Vẽ hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại O như hình 2 :
Hãy điền vào chỗ trống (.......) trong các phát biểu sau :
a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là .........của cạnh Oy'
b) Góc x'Oy và góc xOy' là ...vì cạnh Ox là tia đối của cạnh ..........và cạnh........
Theo dõi (0) 1 Trả lời -
Có bao nhiêu cặp góc đối đỉnh( khác góc bẹt) khi cho n đường thẳng cắt nhau tại một điểm?
bởi Trần Bảo Việt
23/12/2019
a)Cho n đường thẳng cắt nhau tại một điểm hỏi có bao nhiêu cặp góc đối đỉnh( khác góc bẹt)
b) (2x-3)^2=25
Theo dõi (0) 2 Trả lời -
Số cặp góc đối đỉnh khác góc bẹt
bởi Nhat nheo
30/04/2019
Qua điểm O vẽ 20 đường thẳng đôi một phân biệt . Số cặp góc đối đỉnh khác góc bẹt là :
Theo dõi (0) 1 Trả lời -
cho hinh 2. tinh cac goc O1, O2, O3, O4
bởi Bi Bé
18/07/2018
a Góc O1 + Góc O3 =140
b Góc O1 + GócO3 = Góc O2+Góc O4
Theo dõi (0) 1 Trả lời -
help me giải hộ e vs
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB, ta vẽ hai tia OC và OD sao cho \(\widehat {AOC} = \widehat {BOD} = {30^0}\)
a. Hai góc \(\widehat {AOC}\) và \(\widehat {BOD}\) có phải là hai góc đối đỉnh không?
b. Vẽ tia OE sao cho tia OB là tia phân giác của góc DOE. Hai góc AOC và BOE có phải là hai góc đối đỉnh không?
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC vuông tại A ( AB > AC), tia phân giác góc B cắt AC ở D, kẻ DH vuông góc với BC
bởi trang lan
15/03/2018
ai giải hộ em vs, e giải hoài k ra hu hu
Theo dõi (0) 1 Trả lời
