Bài tập 28 trang 35 SGK Hình học 12 NC
Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc \(\alpha \). Thể tích của hình chóp là:
(A) \(\frac{3}{4}{b^3}{\cos ^2}\alpha \sin \alpha \)
(B) \(\frac{{\sqrt 3 }}{4}{b^3}{\cos ^2}\alpha \sin \alpha \)
(C) \(\frac{3}{4}{b^3}\cos \alpha {\sin ^2}\alpha \)
(D) \(\frac{{\sqrt 3 }}{4}{b^3}\cos \alpha \sin \alpha \)
Hướng dẫn giải chi tiết
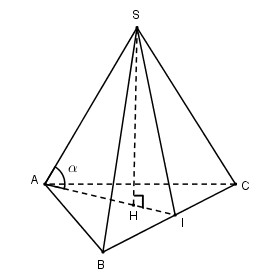
Gọi H là tâm của tam giác đều ABC cạnh a.
\(SH \bot \left( {ABC} \right)\) và \(\widehat {SAH} = \alpha \)
I là trung điểm của BC
\(AH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Trong tam giác vuông AHS có:
\(\begin{array}{l}
\cos \alpha = \frac{{AH}}{{SA}} \Rightarrow b\cos \alpha = \frac{{a\sqrt 3 }}{3}\\
\Rightarrow a = b\sqrt 3 \cos \alpha
\end{array}\)
Diện tích tam giác ABC:
\({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{4}{b^2}{\cos ^2}\alpha \)
Mặt khác \(SH = SA\sin \alpha = b\sin \alpha \)
Thể tích hình chóp là:
\(V = \frac{1}{3}{S_{ABC}}.SH = \frac{{\sqrt 3 }}{4}{b^3}{\cos ^2}\alpha \sin \alpha \)
Chọn (B).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
-
Bài 1.5 trang 11 sách bài tập Hình học 12
bởi thanh duy
24/10/2018
Bài 1.5 (Sách bài tập trang 11)Chứng minh rằng mỗi hình đa diện có ít nhất 4 đỉnh ?
Theo dõi (0) 1 Trả lời -
Bài 1.4 trang 11 sách bài tập Hình học 12
bởi thanh hằng
24/10/2018
Bài 1.4 (Sách bài tập trang 11)
Chia một khối tứ diện đều thành bốn khối tứ diện bằng nhau ?
Theo dõi (0) 1 Trả lời -
Cho hình chóp tứ giác đều S.ABCD, O là tâm mặt phẳng đáy,cạnh đáy là 2a, các cạnh bên tạo với mặt phẳng đáy một góc 60o. Tính khoảng cách giữa SC và BD?
Theo dõi (0) 1 Trả lời -
cho tứ diện đều ABCD cạnh bằng a. tính cosin góc giữa mặt bên và mặt đáy bằng ?
Theo dõi (0) 1 Trả lời -
ADMICRO
Chứng minh DE//CE biết BD= CE
bởi Lê Bảo An
24/10/2018
Tam giác ABC có AB=AC. Trên tia đối của các tia BA và CA lấy 2 điểm D và E sao cho BD= CE
a)CMR: DE//BC
b) từ D kẻ DM vuông góc với BC. Từ E kẻ EN vuông góc với BC. CMR : DM= EN
c) CMR: Tam giác AMN cân
d) từ B và C kẻ các đường vuông góc với AM và AN . chunhs cắt nhau tại I . CMR: AI là tia phân giác chung của 2 góc BAC và MAV
Theo dõi (0) 1 Trả lời -
Cho đường tròn tâm O , bán kính OA=6cm . Gọi H là trung điểm của OA , đường thẳng vuông góc vớ OA tại H cắt đường tròn (O) tại B và C . Kẻ tiếp tuyến với đường tròn (O) tại B , cắt đường thẳng OA tại M.
a) tính độ dài đoạn thẳng MB
b)tứ giác OBAC là hình gì . Vì sao.
c)chứng minh MC là tiếp tuyến của đường tròn (O).
Theo dõi (0) 1 Trả lời -
Tính thể tích khối lăng trụ có đáy là tam giác đều cạnh a, góc giữa cạnh bên và đáy là 60^0
bởi Bin Nguyễn
24/10/2018
Cho lăng trụ ABC.A'B'C' có đáy là tam tác đều cạnh a. Hình chiếu của A' lên (ABC) trùng với trọng tâm của tam giác ABC. Biết góc giữa cạnh bên và mặt đáy bằng 60o.Thể tích khối lăng trụ là?
Theo dõi (0) 1 Trả lời -
Xác định thiết diện của mp alpha với hình chóp S.ABCD có đáy ABCD là hình thang
bởi Nguyễn Thủy Tiên
24/10/2018
Cho hình chóp SABCD; ABCD là hình thang; M là điểm thuộc đoạn BD; mặt phẳng alpha qua M và song song với SA và CB. Xác định thiết diện của alpha với hình chóp.
Theo dõi (0) 1 Trả lời -
Trong không gian với hệ tọa độ Oxyz cho hình hộp chữ nhật ABCD.A'B'C'D' có A trùng với gốc của hệ tọa độ.
B(a;0;0); D(0;a;0); A'(0;0;b); (a>0;b>0)
Gọi M là trung điểm của CC'
a. Tìm thể tích khối tứ diện BDA'M theo a, b
b. Xác định tỉ số \(\frac{a}{b}\) để 2 mặt phẳng (A'BD) và (MBD) vuông góc với nhau.
Theo dõi (0) 1 Trả lời -
Xác định tọa độ các đỉnh của hình vuông ABCD, biết điểm E (2, 3) thuộc BD
bởi Nguyễn Trà Giang
24/10/2018
Cho em hỏi bài này ạ. Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD. Điểm E (2, 3) thuộc BD. Các điểm H (-2, 3) và K (-2,4) lần lượt là hình chiều vuông góc của điểm E trên AB và AD. Xác định tọa độ các đỉnh của hình vuông ABCD
Theo dõi (0) 1 Trả lời
