Trong bài học này, chúng ta sẽ tập trung vào việc tìm hiểu các quy tắc cơ bản để tính đạo hàm của các hàm số. Chúng ta sẽ khám phá cách tính đạo hàm của các hàm số đơn giản như hàm hằng, hàm mũ, hàm số lũy thừa, hàm tổng và hiệu, và hàm hợp. Hãy cùng nhau bắt đầu nào!
Tóm tắt lý thuyết
1.1. Đạo hàm của hàm số \(y = x^n, n\in N^*\)
Hàm số \(y = {x^n}(n \in \mathbb{N},n > 1\)) có đạo hàm với mọi \(x \in\mathbb{R}\) và: \({\left( {{x^n}} \right)'} = n{x^{n - 1}}.\)
1.2. Đạo hàm của hàm số \(y=\sqrt x\)
Hàm số \(y= \sqrt x\) có đạo hàm với mọi x dương và: \(\left( {\sqrt x } \right)' = \frac{1}{{2\sqrt x }}.\)
1.3. Đạo hàm của hàm số lượng giác
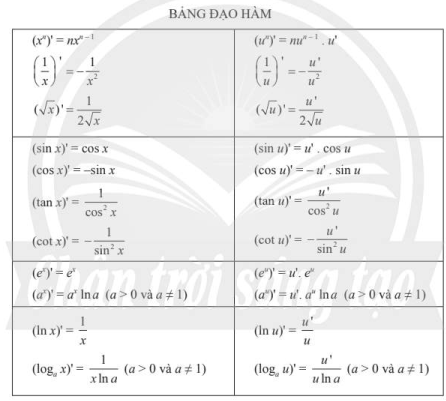
Ta có công thức đạo hàm của các hàm số lượng giác sau:
\(\begin{array}{l}(\sin x)' = \cos x\\ ( \cos x )' = - \sin x\\{\left( {\tan x} \right)'} = \frac{1}{{{{\cos }^2}x}} &\\ {\left( {\cot x} \right)'} = - \frac{1}{{{{\sin }^2}x}} & \end{array}\)
1.4. Đạo hàm của hàm số mũ và hàm số lôgarit
Ta có công thức đạo hàm của các hàm số mũ và hàm số lôgarit sau:
\(\begin{array}{l} \left( {{e^x}} \right)' = {e^x}, \text{với mọi }x \in R \\ \left( {{a^x}} \right)' = {a^x}\ln a,\,\text{với mọi }0 < a \ne 1,\,x \in R \\ \end{array}\)
\(\begin{array}{l} \left( {\ln x} \right)' = \frac{1}{x} \text{với mọi } x\in (0;+\infty)\\\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}} \text{với mọi } x\in (0;+\infty) \\ \end{array}\)
1.5. Đạo hàm của tổng, hiệu, tích, thương của hai hàm số
Cho hai hàm số \(u = u\left( x \right)\) và \(v = v\left( x \right)\) có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
+ \({\left( {u + v} \right)'} = {u'} + {v'}\)
+ \({\left( {u - v} \right)'} = {u'} - {v'}\)
+ \({\left( {u.v} \right)'} = {u'}.v + u.{v'}\) (1)
+ \(\left ( \frac{u}{v} \right )'=\frac{u'v-uv'}{v^2},(v(x) \ne 0)\) (2)
Chú ý: Nếu u = C là một hằng số thì công thức (1) trở thành: \((Cv)'=Cv'.\)
Nếu u = 1 thì công thức (2) trở thành: \({\left( {\frac{1}{v}} \right)'} = - \frac{{ - v'}}{{{v^2}}}\) , \((v(x)\ne 0)\)
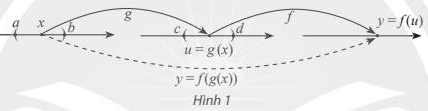
1.6. Đạo hàm của hàm hợp
Hàm số y=f(g(x)) được gọi là hàm hợp của hàm số y=f(u) với u=g(x).
Nếu hàm số u = g(x) có đạo hàm \(u'_x\) tại x và hàm số y = f(u) có đạo hàm \(y'_u\) tại u thì hàm hợp y = f(g(x)) có đạo hàm \(y'_x\) tại x là
1.7. Đạo hàm cấp hai
Hàm số \(y=f(x)\) có đạo hàm tại \(x \in (a;b).\)
- Nếu hàm số \(y'=f'(x)\) có đạo hàm tại x thì ta gọi đạo hàm của y' là đạo hàm cấp hai của hàm số \(y=f(x)\) tại x.
- Kí hiệu: \(y''\) hoặc \(f''(x).\)
Ý nghĩa cơ học của đạo hàm cấp hai
- Đạo hàm cấp hai \(f''(t)\) là gia tốc tức thời của chuyển động có phương trình \(s=f(t)\) tại thời điểm t.
Bài tập minh họa
Câu 1: Tính các đạo hàm của các hàm số sau:
a) y = –x3 + 3x + 1
b) y = (2x – 3)(x5 – 2x)
c) \(y = {x^2}\sqrt x \)
d) \(y = \frac{{2x + 1}}{{1 - 3x}}\)
e) \(y = \frac{{2{x^2} - 4x + 1}}{{x - 3}}\)
Hướng dẫn giải
a) y’ = (–x3 + 3x + 1)’ = –3x2 + 3
b) y = (2x – 3)(x5 – 2x).
y’ = [(2x – 3)(x5 – 2x)]’
= (2x – 3)’.(x5 – 2x) + (x5 – 2x)’.(2x – 3)
= 2(x5 – 2x) + (5x4 – 2)(2x – 3)
= 12x5 – 15x4 – 8x + 6.
c)
\(\begin{array}{l} y = {x^2}\sqrt x \\ y' = {\left( {{x^2}\sqrt x } \right)'}\\ = {\left( {{x^2}} \right)'}.\sqrt x + {\left( {\sqrt x } \right)'}.{x^2}\\ = 2x.\sqrt x + \frac{1}{{2\sqrt x }}.{x^2}\\ = 2x\sqrt x + \frac{1}{2}x\sqrt x \\ = \frac{{5x\sqrt x }}{2} \end{array}\)
d)
\(\begin{array}{l}
y = \frac{{2x + 1}}{{1 - 3x}}\\
\Rightarrow y' = {\left( {\frac{{2x + 1}}{{1 - 3x}}} \right)'}\\
= \frac{{{{\left( {2x + 1} \right)}'}\left( {1 - 3x} \right) - {{\left( {1 - 3x} \right)}'}\left( {2x + 1} \right)}}{{{{\left( {1 - 3x} \right)}^2}}}\\
= \frac{{2\left( {1 - 3x} \right) + 3\left( {2x + 1} \right)}}{{{{\left( {1 - 3x} \right)}^2}}} = \frac{5}{{{{\left( {1 - 3x} \right)}^2}}}
\end{array}\)
e)
\(\begin{array}{l}
y = \frac{{2{x^2} - 4x + 1}}{{x - 3}}\\
\Rightarrow y' = \frac{{{{\left( {2{x^2} - 4x + 1} \right)}'}\left( {x - 3} \right) - {{\left( {x - 3} \right)}'}\left( {2{x^2} - 4x + 1} \right)}}{{{{\left( {x - 3} \right)}^2}}}\\
= \frac{{\left( {4x - 4} \right)\left( {x - 3} \right) - \left( {2{x^2} - 4x + 1} \right)}}{{{{\left( {x - 3} \right)}^2}}} = \frac{{2{x^2} - 12x + 11}}{{{{\left( {x - 3} \right)}^2}}}
\end{array}\)
Câu 2: Tính đạo hàm của các hàm số sau:
a) y = (x7 + x)2
b) y = (1 – 2x2)3
Hướng dẫn giải
a) y = (x7 + x)2. Sử dụng công thức (uα)′=α.uα−1.u' (với u = x7 + x)
y' = 2(x7 + x).(x7 + x)’ = 2(x7 + x)(7x6 + 1).
b) y = (1 – 2x2)3. Sử dụng công thức (uα)' với u = 1 – 2x2
y' = 3(1 – 2x2)2.(1 – 2x2)’ = 3(1 – 2x2)2(– 4x) = – 12x(1 – 2x2)2.
Luyện tập Bài 2 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Tính được đạo hàm một số hàm sơ cấp cơ bản.
- Sử dụng được các công thức tính đạo hàm của tổng, hiệu, tích, thương của các hàm số và đạo hàm của hàm hợp.
- Nhận biết được khái niệm đạo hàm cấp hai, tính được đạo hàm cấp hai của một số hàm đơn giản và giải quyết được một số bài toán thực tiễn.
3.1. Trắc nghiệm Bài 2 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 7 Bài 2 cực hay có đáp án và lời giải chi tiết.
-
Câu 1:
Đạo hàm của hàm số \(f\left( x \right)={{\left( {{x}^{2}}+1 \right)}^{4}}\) tại điểm \(x=-1\) là
- A. 64
- B. 32
- C. -64
- D. -32
-
- A. \(y'={{x}^{5}}-{{x}^{4}}+1+3{{a}^{2}}\).
- B. \(y'={{x}^{5}}-{{x}^{3}}\).
- C. \(y'={{x}^{6}}-{{x}^{4}}\).
- D. \(y'={{x}^{6}}-{{x}^{4}}+3{{a}^{2}}\).
-
- A. 0
- B. -2
- C. -1
- D. 2
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 2 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 7 Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 42 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 1 trang 42 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 1 trang 43 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 2 trang 43 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 43 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 3 trang 43 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 3 trang 44 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 44 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 4 trang 44 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 5 trang 45 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 44 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 6 trang 46 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 6 trang 46 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 7 trang 47 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 7 trang 47 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 8 trang 48 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng trang 48 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 48 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 49 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 49 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 49 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 49 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 49 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 49 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 43 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 43 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 43 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 43 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 43 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 43 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 44 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 8 trang 44 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Hỏi đáp Bài 2 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247