Thực hành 2 trang 100 SGK Toán 10 Chân trời sáng tạo tập 1
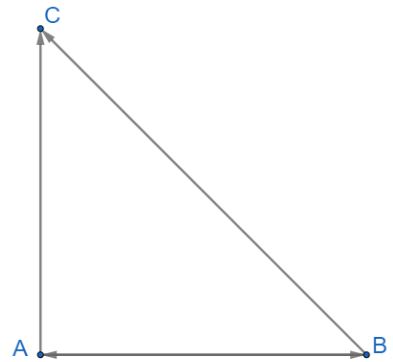
Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng \(\sqrt 2 \).
Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {BC} ,\overrightarrow {BA} .\overrightarrow {BC} \)
Hướng dẫn giải chi tiết Thực hành 2
Phương pháp giải
Bước 1: Vận dụng công thức \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
Bước 2: Xác định độ dài cạnh AB, AC và góc giữa hai vecto \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)
Lời giải chi tiết
+) Ta có: \(AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
+) \(\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)\)
Ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \)\( \Rightarrow AC = 1\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
+) \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Thực hành 1 trang 99 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 98 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 100 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 100 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 100 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 100 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Trên mặt phẳng tọa độ Oxy cho ba điểm A(2; 4), B(1; 2), C(6; 2). Hãy chứng minh \(\overrightarrow {AB} \bot \overrightarrow {AC} \)
bởi Nguyễn Thanh Thảo
 05/09/2022
Theo dõi (0) 1 Trả lời
05/09/2022
Theo dõi (0) 1 Trả lời