Thực hành 1 trang 99 SGK Toán 10 Chân trời sáng tạo tập 1
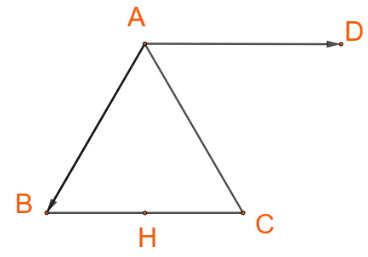
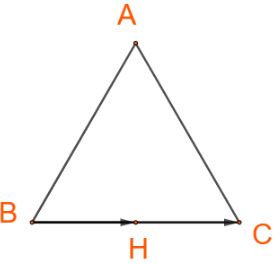
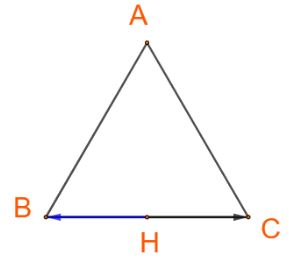
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\).
Hướng dẫn giải chi tiết Thực hành 1
Phương pháp giải
Bước 1: Xác định hai vectơ cần tìm góc
Bước 2: Đưa 2 vectơ về cùng điểm đầu (chung gốc)
Bước 3: Xác định góc giữa 2 vectơ, chẳng hạn: \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)
Lời giải chi tiết
+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)
+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Hoạt động khám phá 1 trang 98 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 98 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 100 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 100 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 100 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 100 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 100 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Trên mặt phẳng \(Oxy\), cho hai điểm là \(A(1; 3), \, B(4;2)\). Chứng tỏ rằng \(OA\) vuông góc với \(AB\) và từ đó tính diện tích tam giác \(OAB.\)
bởi Hoang Viet
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời