Hoạt động khám phá 2 trang 89 SGK Toán 10 Chân trời sáng tạo tập 1
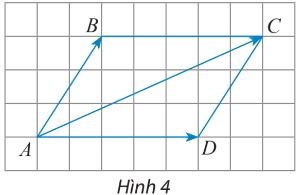
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Hướng dẫn giải chi tiết Hoạt động khám phá 2
Phương pháp giải
Tìm vectơ bằng với vectơ \(\overrightarrow {AD} \), sau đó áp dụng quy tắc ba điểm
Lời giải chi tiết
Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Hoạt động khởi động trang 88 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 88 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 89 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 89 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 90 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 90 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 90 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 91 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 91 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 92 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 92 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 5 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Chứng minh mệnh đề cho sau đây: Nếu \(\overrightarrow a + \overrightarrow b = \overrightarrow c \) thì \(\overrightarrow a = \overrightarrow c - \overrightarrow b ,\overrightarrow b = \overrightarrow c - \overrightarrow a \)
bởi thu hằng
 05/09/2022
Theo dõi (0) 1 Trả lời
05/09/2022
Theo dõi (0) 1 Trả lời