Thực hành 5 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1
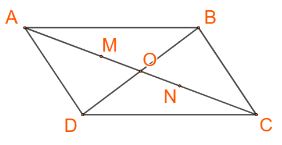
Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:
a) \(\overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {MB} = \overrightarrow 0 \)
b) \(\overrightarrow {ND} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
c) \(\overrightarrow {PM} + \overrightarrow {PN} = \overrightarrow 0 \)
Hướng dẫn giải chi tiết Thực hành 5
Phương pháp giải
a) Sử dụng tính chất trọng tâm của tam giác \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)(với G là trọng tâm của tam giác ABC)
b) Sử dụng tính chất trọng tâm của tam giác \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
c) Sử dụng tính chất trung điểm \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)(với M là trung điểm của AB)
Lời giải chi tiết
a) Áp dụng tính chất trọng tâm ta có: \(\overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {MB} = \overrightarrow 0 \)
Suy ra M là trọng tâm của tam giác ADB
Vậy M nằm trên đoạn thẳng AO sao cho \(AM = \frac{2}{3}AO\)
b) Tiếp tục áp dụng tính chất trọng tâm \(\overrightarrow {ND} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)
Suy ra N là trọng tâm của tam giác BCD
Vậy N nằm trên đoạn thẳng OD sao cho \(ON = \frac{1}{3}OD\)
c) Áp dụng tính chất trung điểm ta có: \(\overrightarrow {PM} + \overrightarrow {PN} = \overrightarrow 0 \)
Suy ra P là trung điểm của đoạn thẳng MN
Vậy điểm P trùng với điểm O
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Thực hành 4 trang 92 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 92 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Cho \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow 0 \). Chứng tỏ \(\overrightarrow {BC} \) là vectơ đối của \(\overrightarrow {AB} \)
bởi Trần Hoàng Mai
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời