Hoạt động khám phá 2 trang 90 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
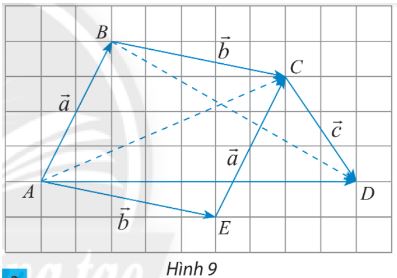
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:
a) \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = ?\)
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = ?\)
b) \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = ?\)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = ?\)
Hướng dẫn giải chi tiết Hoạt động khám phá 2
Phương pháp giải
Bước 1: Áp dụng quy tắc 3 điểm: \( \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
Bước 2: So sánh các vectơ vừa tìm được
Lời giải chi tiết
a) Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \); \(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = \overrightarrow {AC} \)
\( \Rightarrow \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
a) Áp dụng quy tắc ba điểm ta có:
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Vận dụng 1 trang 90 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 90 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 91 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 91 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 92 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 92 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 5 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Cho biết hình bình hành \(ABCD\) với tâm \(O\). Hãy điền vào chỗ trống (…) để được đẳng thức đúng: \(\overrightarrow {AB} + \overrightarrow {AD} = ....\)
bởi Lan Anh
 05/09/2022
Theo dõi (0) 1 Trả lời
05/09/2022
Theo dõi (0) 1 Trả lời