Hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Chương 1 Bài 3 Các phép toán trên tập hợp giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 21 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Có hai đường tròn chia một hình chữa nhật thành các miền như hình bên. Hãy đặt mỗi thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm.
-
Hoạt động khám phá 1 trang 21 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):
a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.
c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.
-
Thực hành 1 trang 23 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Xác định các tập hợp \(A \cup B\) và \(A \cap B\), biết:
a) \(A = \{ a;b;c;d;e\} \), \(B = \{ a;e;i;u\} \)
b) \(A = \{ x \in \mathbb{R}|\;{x^2} + 2x - 3 = 0\} \),\(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \)
-
Thực hành 2 trang 23 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x - y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x - y = 1\} \)
Hãy xác định \(A \cap B\).
- VIDEOYOMEDIA
-
Vận dụng trang 23 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tại vòng chung kết của một trò chơi truyền hình, có 100 khán giải tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rẳng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh này. Có bao nhiêu khán giá đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?
-
Hoạt động khám phá 2 trang 23 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.
a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.
-
Thực hành 3 trang 24 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)
Xác định các tập hợp sau đây:
a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\)
b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\)
c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\)
-
Thực hành 4 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Xác định các tập hợp sau đây:
a) \((1;3) \cup [ - 2;2]\)
b) \(( - \infty ;1) \cap [0;\pi ]\)
c) \([\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\)
d) \({C_\mathbb{R}}[ - 1; + \infty )\)
-
Giải bài 1 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Xác định các tập hợp \(A \cup B\) và \(A \cap B\) với
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; làm; chàm; tím}.
b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
-
Giải bài 2 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Xác định các tập hợp \(A \cap B\) trong mỗi trường hợp sau:
a) \(A = \{ x \in \mathbb{R}|{x^2} - 2 = 0\} ,\)\(B = \{ x \in \mathbb{R}|2x - 1 < 0\} \)
b) \(A = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1\} ,\)\(B = \{ (x;y)|\;x,y \in \mathbb{R},y = - x + 5\} \)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
-
Giải bài 3 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho \(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|x\)là bội của 3\(\} ,\)\(B = \{ x \in E|x\) là ước của 6\(\} .\)
Xác định các tập hợp \(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
-
Giải bài 4 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
a) A và \(A \cup B\)
b) A và \(A \cap B\)
-
Giải bài 5 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
a) Có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) Có bao nhiêu học sinh không thích cả hai môn này?
-
Giải bài 6 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Xác định các tập hợp sau đây:
a) \(( - \infty ;0) \cup [ - \pi ;\pi ]\)
b) \([ - 3,5;2] \cap ( - 2;3,5)\)
c) \(( - \infty ;\sqrt 2 ] \cap [1; + \infty )\)
d) \(( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)
-
Giải bài 1 trang 16 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Xác định \(A \cap B,A \cup B,A\backslash B,B\backslash A\) trong các trường hợp sau:
a) \(A = \left\{ {a;b;c;d} \right\},B = \left\{ {a;c;e} \right\}\)
b) \(A = \left\{ {x\left| {{x^2} - 5x - 6 = 0} \right.} \right\},B = \left\{ {x\left| {{x^2} = 1} \right.} \right\}\)
c) \(A= \{ x \in \mathbb N | x\) là số lẻ, \(x<8\) , \(B =\{ x \in \mathbb N | x\) là các ước của 12}
-
Giải bài 2 trang 16 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hai tập hợp \(A = \left\{ {\left( {x;y} \right)\left| {3x - 2y = 11} \right.} \right\},B = \left\{ {\left( {x;y} \right)\left| {2x + 3y = 3} \right.} \right\}\). Hãy xác định tập hợp \(A \cap B\)
-
Giải bài 3 trang 16 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho các tập hợp \(A = \left\{ {1;3;5;7;9} \right\},B = \left\{ {1;2;3;4} \right\},C = \left\{ {3;4;5;6} \right\}\). Hãy xác định các tập hợp
a) \(\left( {A \cup B} \right) \cap C\)
b) \(A \cap \left( {B \cap C} \right)\)
c) \(A\backslash \left( {B \cap C} \right)\)
d) \(\left( {A\backslash B} \right) \cup \left( {A\backslash C} \right)\)
-
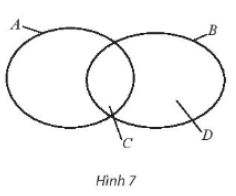
Giải bài 4 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Kí hiệu A là tập hợp các học sinh nữ của trường, B là tập hợp các học sinh khối 10 của trường; C, D lần lượt là tập hợp các học sinh nữ, các học sinh nam khối 10 của trường ̣̣̣( hình 7). Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm
a) \(A \cap B = ...\)
b) \(C \cup D = ...\)
c) \(B\backslash A = ...\)
d) \(B \cap C = ...\)
e) \(C\backslash A = ...\)
g) \(D\backslash A = ...\)
-
Giải bài 5 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho A là tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm
a) \(A \cap A = ...\)
b) \(A \cup A = ...\)
c) \(A \cap \emptyset = ...\)
d) \(A \cup \emptyset = ...\)
e) \(A\backslash A = ...\)
g) \(A\backslash \emptyset = ...\)
h) \(\emptyset \backslash A = ...\)
-
Giải bài 6 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm
a) Nếu \(B \subset A\) thì \(A \cap B = ...,A \cup B = ...\) và \(B\backslash A = ...\)
b) Nếu \(A \cap B = \emptyset \) thì \(A\backslash B = ...\) và \(B\backslash A = ...\)
-
Giải bài 7 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho các tập con \(A = \left[ { - 1;3} \right]\) và \(B = \left[ {0;5} \right)\) của tập số thực \(\mathbb{R}\)
Hãy xác định \(A \cap B,A \cup B,A\backslash B,B\backslash A\)
-
Giải bài 8 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Lớp 10E có 18 bạn chơi cầu lông, 15 bạn chơi cờ vua, 10 bạn chơi cả hai môn và 12 bạn không chơi môn nào trong hai môn thể thao này
a) Lớp 10E có bao nhiêu bạn chơi ít nhất một môn thể thao trên?
b) Lớp 10E có bao nhiêu học sinh?
-
Giải bài 9 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Biết rằng tập hợp M thỏa mãn \(M \cap \left\{ {1;3} \right\} = \left\{ 1 \right\},M \cap \left\{ {5;7} \right\} = \left\{ 5 \right\},M \cap \left\{ {9;11} \right\} = \left\{ 9 \right\}\)và \(M \subset \left\{ {1;3;5;7;9;11} \right\}\). Hãy tìm M
-
Giải bài 10 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tập hợp \(A = \left\{ {1;2;3} \right\}\)
a) Tìm tất cả các tập hợp B sao cho \(A \cup B = A\)
b) Tìm tất cả các tập hợp C sao cho \(A \cap C = C\)
-
Giải bài 11 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho \(U = \left\{ {3;5;{a^2}} \right\},A = \left\{ {3;a + 4} \right\}\). Tìm giá trị của a sao cho \({C_U}A = \left\{ 1 \right\}\)





.JPG)

.JPG)