Thực hành 4 trang 25 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST

Hướng dẫn giải

Sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a < b)

Lời giải chi tiết

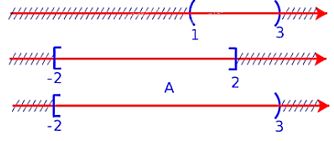
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy \(A = [ - 2;3)\)

b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy \(B = [0;1)\)

 c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)

d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)

-- Mod Toán 10 HỌC247