Giải bài 7 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1
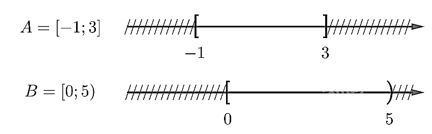
Cho các tập con \(A = \left[ { - 1;3} \right]\) và \(B = \left[ {0;5} \right)\) của tập số thực \(\mathbb{R}\)
Hãy xác định \(A \cap B,A \cup B,A\backslash B,B\backslash A\)
Hướng dẫn giải chi tiết Bài 7
Phương pháp giải
\(\left[ {a;b} \right]=\left\{ {x \in \mathbb{R}\left| {a \le x \le b} \right.} \right\}\)
\(\left( {a;b} \right)=\left\{ {x \in \mathbb{R}\left| {a < x < b} \right.} \right\}\)
\(\left[ {a;b} \right)=\left\{ {x \in \mathbb{R}\left| {a \le x < b} \right.} \right\}\)
\(A \cap B = \{x | x \in A \) và \(x \in B \}\)
\(A \cup B = \{x | x \in A \) hoặc \(x \in B \}\)
\(A\backslash B = \{x | x \in A \) và \(x \notin B \}\)
Lời giải chi tiết
\(\begin{array}{l}A \cap B = \left[ {0;3} \right], \\ A \cup B = \left[ { - 1;5} \right),\\A\backslash B = \left[ { - 1;0}
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 5 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 17 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.