-
Câu hỏi:
Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh BC.
-
A.
\(BC = 3 + 3\sqrt 6 ;\)
-
B.
\(BC = 3\sqrt 6 - 3;\)
-
C.
\(BC = 3\sqrt 7 \)
-
D.
\(BC = \frac{{3 + 3\sqrt {33} }}{2}.\)
Lời giải tham khảo:
Đáp án đúng: A
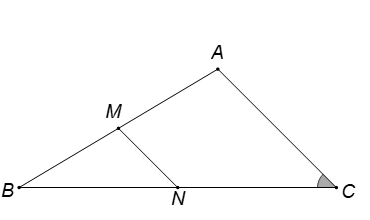
Gọi M, N lần lượt là trung điểm của AB, BC.
=> MN là đường trung bình của ΔABC
\(\Rightarrow MN = \frac{1}{2}AC\). Mà MN = 3, suy ra AC = 6.
Theo định lí hàm cosin, ta có:
\(\begin{array}{l}
A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\\
\Leftrightarrow {9^2} = {6^2} + B{C^2} - 2.6.BC.\cos 60^\circ \\
\Leftrightarrow B{C^2} - \;6.BC - 45 = 0\\
\Leftrightarrow BC = 3 + 3\;\sqrt 6
\end{array}\)Đáp án đúng là: A
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Tam giác đều ABC có đường cao AH. Khẳng định cho nào sau đây là đúng?
- Tính giá trị biểu thức sau \(P = \sin 30^\circ \cos 15^\circ + \sin 150^\circ \cos 165^\circ .\)
- Cho biết sinα + cosα = a. Hãy tính giá trị của sinα.cosα
- Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và \(\widehat {ACB} = 60^\circ \). Hãy tính độ dài cạnh cạnh BC.
- Tam giác ABC có \(AB = \sqrt 2 ,AC = \sqrt 3 \) và \(\widehat C = {45^0}\). Hãy tính độ dài cạnh BC
- Tam giác ABC có \(\widehat B = 60^\circ ,\widehat C = 45^\circ \) và AB = 5. Hãy tính độ dài cạnh AC.
- Cho hình thoi ABCD cạnh bằng 1cm và có \(\widehat {BAD} = {60^0}\). Hãy tính độ dài AC.
- Cho tam giác ABC, biết AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp của tam giác ABC bằng
- Cho tam giác ABC có a = 5, b = 6, c = 7. Tính diện tích của tam giác ABC
- Cho biết tam giác ABC có a = 3, b = 5, c = 6. Bán kính đường trong nội tiếp của tam giác bằng
VIDEO
YOMEDIA
ADMICRO
