-
Câu hỏi:
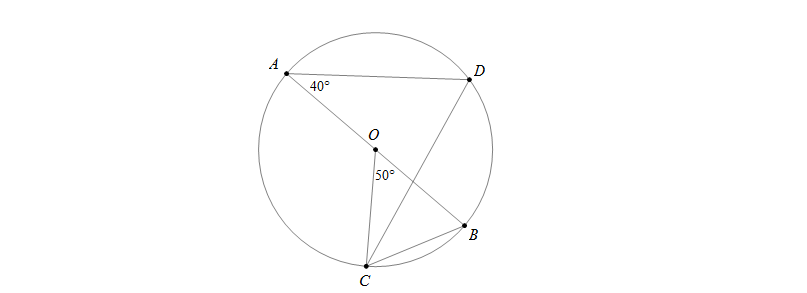
Số đó góc OCD trên hình vẽ là:
-
A.
250
-
B.
150
-
C.
200
-
D.
100
Lời giải tham khảo:
Đáp án đúng: A

Ta có \(\widehat{BAD}=\widehat{BCD}=40^0\) (hai góc nội tiếp cùng chắn cung BD)
Tam giác OBC cân tại O có \(\widehat{BOC}=50^0\) nên \(\widehat{BCO}=\frac {180^0-50^0}{2}=65^0\)
Lúc đó \(\widehat{OCD}=\widehat{OCB}-\widehat{BCD}=65^0-40^0=25^0\).
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Chỉ ra khẳng định đúng trong các khẳng định sau:
- Dựa vào hình vẽ sau, biết rằng widehat{AOB}=130^0,widehat{ADO}=40^0) và sđ(stackrelfrown{CD} =30^0. Số đo góc BAC là:
- Dựa vào hình sau, biết AB,CD là hai dây của đường tròn (O), M là điểm chính giữa cung nhỏ AB. Khẳng định nào sau đây là sai:
- Số đó góc OCD trên hình vẽ là:
- Cho đường tròn (O) có đường kính AB bằng 12cm. Một đường thẳng qua A cắt đường tròn (O) ở M và cắt tiếp tuyến của đường tròn tại B ở N.




