-
Câu hỏi:
Cho hàm số \(y=f\left( x \right)\), hàm số \(y={f}'\left( x \right)\) liên tục trên \(R\) và có đồ thị như hình vẽ.
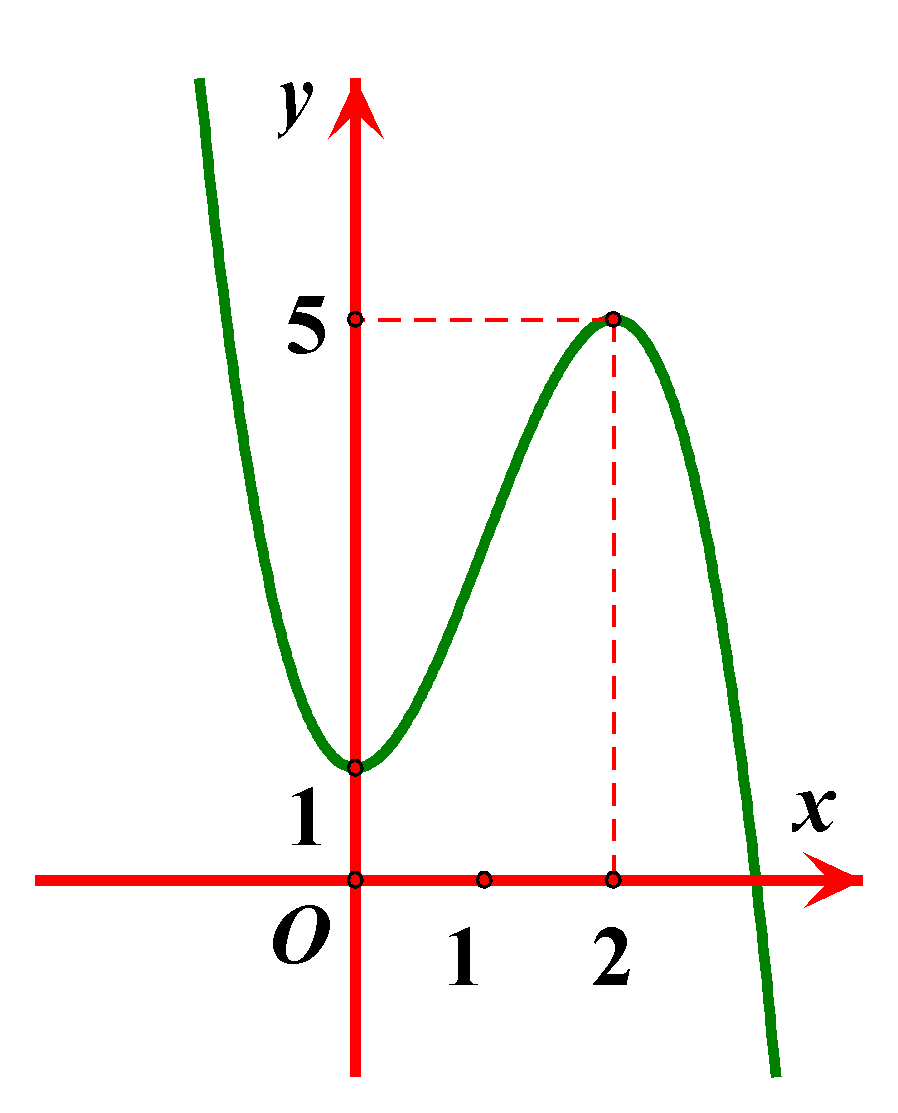
Bất phương trình \(f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1\) (với \(m\) là tham số thực) nghiệm đúng với mọi \(x\in \left( 0\,;\,3 \right)\) khi và chỉ khi
-
A.
\(m<f\left( 3 \right)-24\).
-
B.
\(m<f\left( 0 \right)\).
-
C.
\(m\le f\left( 3 \right)-24\).
-
D.
\(m\le f\left( 0 \right)\).
Lời giải tham khảo:
Đáp án đúng: C
T a có \(f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1,\,\forall \,x\in \left( 0\,;\,3 \right)\)
\(\Leftrightarrow f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right)>m,\,\forall \,x\in \left( 0\,;\,3 \right)\) \(\Leftrightarrow m<\underset{\left( 0\,;\,3 \right)}{\mathop{\min }}\,\left[ f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right) \right],\,\forall \,x\in \left( 0\,;\,3 \right)\)
Đặt \(h\left( x \right)=f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right)\)
Có \({h}'\left( x \right)={f}'\left( x \right)-\left( 3{{x}^{2}}-6x+8 \right)={f}'\left( x \right)-\left[ 3{{\left( x-1 \right)}^{2}}+5 \right]\).
Từ đồ thị ta thấy trên khoảng \(\left( 0\,;\,3 \right)\) thì \({f}'\left( x \right)\le 5\). Mặt khác \(\left[ 3{{\left( x-1 \right)}^{2}}+5 \right]\ge 5\) nên \({h}'\left( x \right)\le 0,\,\forall \in \left( 0\,;\,3 \right)\).
Ta có hàm số \(y=h\left( x \right)\) nghịch biến trên khoảng \(\left( 0\,;\,3 \right)\) nên từ \(m<\underset{\left( 0\,;\,3 \right)}{\mathop{\min }}\,\left[ f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right) \right],\,\forall \,x\in \left( 0\,;\,3 \right)\Leftrightarrow m\le f\left( 3 \right)-24\).
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho \(f\left( 1 \right)=2\) và \(\int\limits_{1}^{3}{{f}'\left( x \right)dx}=6\) tính \(f\left( 3 \right)\)
- Nghiệm của phương trình \({{2}^{2x-1}}=8\) là gì
- Tiệm cận đứng của đồ thị hàm số \(y=\frac{2x-1}{x+1}\) là đường thẳng có phương trình
- Trong hình vẽ dưới đây, điểm \(M\) là điểm biểu diễn của số phức nào?
- Trong không gian \(Oxyz\), phương trình nào dưới đây là phương trình của mặt cầu tâm \(I\left( 1;\ 0;\ -2 \right),\) bán kính \(R=4?\)
- Tập xác định của hàm số \(y=\ln \left( 2-x \right)\) là
- Cho hình hộp đứng có đáy là hình vuông cạnh bằng \(a,\) độ dài cạnh bên bằng \(3a.\) Thể tích của khối hộp đã cho bằng
- Một nguyên hàm của hàm số \(f\left( x \right)=\sin \left( 2x-\frac{\pi }{3} \right)\) là
- Một cấp số nhân gồm ba số hạng, biết số hạng thứ nhất và thứ hai lần lượt là \(-1;\,3.\) Số hạng cuối của cấp số nhân đó bằng
- Trong không gian \(Oxyz,\) mặt phẳng \(\left( \alpha \right):-2x+3y-z+5=0\) đi qua điểm nào dưới đây?
- Cho mặt cầu có đường kính bằng \(8.\) Diện tích của mặt cầu đã cho bằng
- Biết \({\int\limits_{0}^{1}{f\left( x \right)\text{d}x=-2}}\) và \({\int\limits_{0}^{5}{f\left( x \right)\text{d}x=3},}\) khi đó \({\int\limits_{1}^{5}{2f\left( x \right)\text{d}x}}\) bằng
- Cho hai số phức \({{z}_{1}}=1-2i\) và \({{z}_{2}}=3+4i.\) Số phức \({{z}_{1}}.{{z}_{2}}\) bằng
- Đồ thị hàm số \(y=\frac{x-4}{2x+2}\) cắt trục tung tại điểm có tung độ bằng
- Trong không gian \(Oxyz,\) đường thẳng \(d:\left\{ \begin{align} & x=1-t \\ & y=2+2t \\ & z=3-t \\ \end{align} \right.\)
- Đạo hàm của hàm số \(y={{5}^{2x}}\) là
- Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
- Tập nghiệm của bất phương trình \({{\log }_{3}}\left( x-2 \right)\le 2\) là
- Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
- Cho khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=2.\) Thể tích của khối chóp đã cho bằng
- Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y=\ln x\), \(y=0\), \(x=1\), \(x=e\). Mệnh đề nào dưới đây đúng?
- Số cách xếp \(5\) người thành một hàng ngang là
- Số phức liên hợp của số phức \(z=-2+3i\) là số phức nào dưới đây
- Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ bên
- Lấy ngẫu nhiên một số tự nhiên nhỏ hơn \(100,\) xác suất để lấy được một số chia hết cho \(6\) bằng
- Hàm số \(y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-6x+\frac{5}{6}\) đồng biến trên khoảng
- Tính tích phân \(I=\int\limits_{1}^{5}{\frac{1}{\sqrt{2x-1}+1}\text{d}x}\) bằng cách đặt \(u=\sqrt{2x-1}\), mệnh đề nào dưới đây đúng?
- Cho ba điểm \(A\left( 1;2;-1 \right),\,\,B\left( 2;-1;3 \right),\,\,C\left( -3;5;1 \right).\)
- Cho hai số phức \({{z}_{1}}=3+i\) và \({{z}_{2}}=2-i.\) Tính \(T=\left| {{z}_{1}}+{{z}_{1}}{{z}_{2}} \right|.\)
- Trong không gian \(Oxyz,\) cho hai điểm \(A\left( 1;-2;-3 \right),\,\,B\left( -1;4;1 \right)\) và đường thẳng \(d:\frac{x+2}{1}=\frac{y-2}{-1}=\frac{z+3}{2}.\)
- Giá trị lớn nhất của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+25\) trên đoạn \(\left[ -2;2 \right]\) bằng
- Cho hàm số \(y=f\left( x \right)\) có đồ thị \(y={f}'\left( x \right)\) cắt trục \(Ox\) tại ba điểm có hoành độ \(a,b,c\) như hình vẽ
- Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi M là trung điểm SD
- Tổng các nghiệm của phương trình \({{\log }_{\sqrt{2}}}\left( x-1 \right)+\log \left( x+3 \right)=1\) bằng
- Cho hàm số đa thức bậc bốn \(y=f\left( x \right)\), đồ thị của hàm số \(y={f}'\left( 1-x \right)\) là đường cong ở hình vẽ.
- Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng \(a,\) cạnh bên bằng \(a\sqrt{2}.\) Gọi \(M\) là trung điểm cạnh \(AC.\)
- Cho hàm số \(y=f(x)\) có đạo hàm là \({f}'(x)=\ln \left( x+a \right),\forall x>-a,\,\ a\) là số thực dương và \(f(0)=a\ln a\).
- Cho \(g\left( x \right)={{x}^{2}}-2x-1\) và hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AD=2\sqrt{2},\,\,AB=1,\,\,\)
- Cho hàm số \(y=f\left( x \right)\), hàm số \(y={f}'\left( x \right)\) liên tục trên \(R\) và có đồ thị như hình vẽ.
- Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ: Số giá trị nguyên của tham số \(m\) để hàm số
- Cho hai số phức \({{z}_{1}},\,\,{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}+2-i \right|+\left| {{z}_{1}}-4-7i \right|=6\sqrt{2}\) và \(\left| i{{z}_{2}}-1+2i \right|=1.\)
- Cho hình nón đỉnh \(S,\) đáy là hình tròn tâm \(O,\) góc ở đỉnh của hình nón là \(\varphi =120{}^\circ .\) Cắt hình nón bởi mặt phẳng đi qua đỉnh \(S\)
- Trong không gian \(Oxyz,\)cho mặt phẳng \(\left( P \right):2x-y+z-10=0\) và \(d:\frac{x+2}{2}=\frac{y-1}{1}=\frac{z-1}{-1}.\)
- Cho phương trình\({{z}^{2}}+az+2{{a}^{2}}=0\), với \(a\) là số thực dương. Gọi \({{z}_{1}},{{z}_{2}}\) là hai nghiệm phức của phương trình
- Có bao nhiêu giá trị nguyên \({b>1}\) để với mỗi giá trị của \({b}\) có đúng 5 số nguyên
- Cho hàm số \(f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)\) có đồ thị là đường cong \(\left( C \right)\)
- Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\) đường thẳng \(d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\)
- Cho hàm số bậc ba \(y=f\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+\frac{1}{3}x+q\) có đồ thị \(\left( C \right)\) và cắt đường thẳng \(d:y=g\left( x \right)\) như hình vẽ
- Cho hàm số bậc ba \(f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d\) có đồ thị như hình vẽ dưới đây


