Đội ngũ giáo viên HOC247 xin gửi đến quý thầy, cô giáo và các em học sinh nội dung Đề thi giữa HK2 môn Toán 10 KNTT năm 2022-2023 Trường THPT Lê Quý Đôn có đáp án nhằm phục vụ nhu cầu tham khảo và luyện giải đề. Với cấu trúc trắc nghiệm và đáp án đầy đủ sẽ giúp các em cập nhật cấu trúc đề thi và đơn vị kiến thức quan trọng cho kì thi giữa học kì 2 quan trọng sắp đến. Mời các em cùng tham khảo nhé!
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG THPT LÊ QUÝ ĐÔN
|
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KÌ 2 NĂM HỌC 2022-2023 MÔN TOÁN LỚP 10 Thời gian làm bài : 60 phút |
|
|
Đề thi gồm 2 trang |
A. Đề bài
Câu 1. Cho hàm số \(y=f\left( x \right)=a{{x}^{2}}+bx+c\) có đồ thị như hình bên. Dấu của hệ số \(a\) và biệt thức \(\text{ }\!\!\Delta\!\!\text{ }\) là
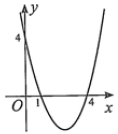
A. \(a>0,\text{ }\!\!\Delta\!\!\text{ }>0\).
B. \(a<0,\,\Delta >0\).
C. \(a>0,\text{ }\!\!\Delta\!\!\text{ }=0\).
D. \(a<0,\text{ }\!\!\Delta\!\!\text{ }=0\).
Câu 2. Bất phương trình nào sau đây có tập nghiệm là \(S=\mathbb{R}\setminus \left\{ 2 \right\}\) ?
A. \({{x}^{2}}+4x+5\le 0\).
B. \(-2{{x}^{2}}+5x-11>0\).
C. \(-3{{x}^{2}}+12x-12<0\).
D. \(-3{{x}^{2}}+12x-12\ge 0\).
Câu 3. Giá trị của tham số \(m\) để phương trình \({{x}^{2}}-\left( m+1 \right)x+4=0\) có nghiệm là
A. \(\left( -5;3 \right)\).
B. \(\left( -\infty ;-5\left] \cup \right[3;+\infty \right)\).
C. \(\left[ -5;3 \right]\).
D. \(\left( -\infty ;-5 \right)\cup \left( 3;+\infty \right)\).
Câu 4. Cho tam thức bậc hai \(f\left( x \right)=m{{x}^{2}}+2x+m\). Giá trị của tham số \(m\) để \(f\left( x \right)\ge 0\forall x\in \mathbb{R}\) là
A. \(m\ge 1\).
B. \(m>1\).
C. \(m>0\).
D. \(m<2\).
Câu 5. Cho bất phương trình \(-{{x}^{2}}-2mx+{{m}^{2}}-2m\le 0\). Giá trị của \(m\) để bất phương trình có nghiệm đúng với mọi \(x\in \mathbb{R}\) là
A. \(0\le m\le 1\).
B. \(0\)
Câu 6. Tập nghiệm của bất phương trình \(\frac{2{{x}^{2}}-3x+4}{{{x}^{2}}+2}>1\) là
A. \(\left( -\infty ;-1 \right)\cup \left( 2;+\infty \right)\).
B. \(\left( -\infty ;-2 \right)\cup \left( -1;+\infty \right)\).
C. \(\left( -\infty ;1 \right)\cup \left( 2;+\infty \right)\).
D. \(\left( -\infty ;2 \right)\cup \left( 4;+\infty \right)\).
Câu 7. Tam thức bậc hai \(f\left( x \right)=-{{x}^{2}}+5x-6.f\left( x \right)>0\) khi và chỉ khi
A. \(x\in \left( -\infty ;2 \right)\).
B. \(\left( 3;+\infty \right)\).
C. \(x\in \left( 2;+\infty \right)\).
D. \(x\in \left( 2;3 \right)\).
Câu 8. Số giá trị nguyên của \(x\) để \(2{{x}^{2}}-7x-9<0\) là
A. 3 .
B. 4 .
C. 5 .
D. 6 .
Câu 9. Bảng xét dấu nào sau đây là của tam thức \(f\left( x \right)=-{{x}^{2}}+4x-4\) ?
A.

B.

C.

D.

Câu 10. Tìm tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{*{35}{l}} {{x}^{2}}-4x+3>0 \\ {{x}^{2}}-6x+8>0 \\ \end{array} \right.\).
A. \(\left( -\infty ;1 \right)\cup \left( 3;+\infty \right)\).
B. \(\left( -\infty ;1 \right)\cup \left( 4;+\infty \right)\).
C. \(\left( -\infty ;2 \right)\cup \left( 3;+\infty \right)\).
D. \(\left( 1;4 \right)\).
Câu 11. Cho bất phương trình \({{x}^{2}}+4x+\left| x+2 \right|-m\le 0\). Xác định \(m\) để bất phương trình có nghiệm.
A. \(-\frac{17}{4}\le m\le -4\).
B. \(m\le -4\).
C. \(m\ge -\frac{17}{4}\).
D. \(m\ge -4\).
Câu 12. Cho phương trình \(\left( m-5 \right){{x}^{2}}+2\left( m-1 \right)x+m=0\) (1). Với giá trị nào của \(m\) thì (1) có 2 nghiệm \({{x}_{1}},{{x}_{2}}\) thỏa \({{x}_{1}}<1<{{x}_{2}}\) ?
A. \(m\ge 5\).
B. \(m<\frac{7}{4}\).
C. \(\frac{7}{4}\)
Câu 13. Điều kiện xác định của phương trình \(\sqrt{x-1}+\sqrt{x-2}=\sqrt{x-3}\) là:
A. \(\left( 3;+\infty \right)\).
B. \(\left[ 2;+\infty \right)\).
C. \(\left[ 1;+\infty \right)\).
D. \(\left[ 3;+\infty \right)\).
Câu 14. Phương trình sau có bao nhiêu nghiệm \(\sqrt{x}=\sqrt{-x}\) ?
A. 0 .
B. 1 .
C. 2 .
D. vô số.
Câu 15. Tập nghiệm của phương trình \(x-\sqrt{x-3}=\sqrt{3-x}+3\) là:
A. \(S=\varnothing \).
B. \(S=\left\{ 3 \right\}\).
C. \(S=\left[ 3;+\infty \right)\).
D. \(S=\mathbb{R}\).
Câu 16. Phương trình \(\sqrt{f\left( x \right)}=\sqrt{g\left( x \right)}\) tương đương với phương trình nào sau đây?
A. \(f\left( x \right)=g\left( x \right)\).
B. \({{f}^{2}}\left( x \right)={{g}^{2}}\left( x \right)\).
C. \(\left[ \begin{array}{*{35}{l}} f\left( x \right) > 0 \\ f\left( x \right)=g\left( x \right) \\ \end{array} \right.\).
D. \(\left\{ \begin{array}{*{35}{l}} f\left( x \right)\ge 0 \\ f\left( x \right)=g\left( x \right) \\ \end{array} \right.\).
Câu 17. Phương trình \({{(x-4)}^{2}}=x-2\) là phương trình hệ quả của phương trình nào sau đây?
A. \(x-4=x-2\).
B. \(\sqrt{x-2}=x-4\).
C. \(\sqrt{x-4}=\sqrt{x-2}\).
D. \(\sqrt{x-4}=x-2\).
Câu 18. Số giá trị nguyên của \(m\) để phương trình \(\sqrt{{{x}^{2}}-x+m}=\sqrt{x-3}\) có hai nghiệm phân biệt là
A. 0 .
B. 1.
C. 2 .
D. 3 .
Câu 19. Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec{a}=\left( -4;2 \right),\vec{b}=\left( 2k;-k \right)\). Với giá trị nào của \(k\) dưới đây thì \(\vec{a}=\vec{b}?\)
A. \(k=-\frac{1}{2}\).
B. \(k=2\).
C. \(k=-2\).
D. Không tồn tại \(k\).
Câu 20. Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec{a}=\left( -m+2n;-1 \right),\vec{b}=\left( 5;-m-n \right)\). Với giá trị nào của \(m,n\) dưới đây thì \(\vec{a}=\vec{b}\) ?
A. \(m=-1,n=2\).
B. \(m=2,n=-1\).
C. \(m=2,n=1\).
D. Không tồn tại \(m,n\).
Câu 21. Trong mặt phẳng toạ độ \(Oxy\), cho \(A\left( 2;-3 \right),B\left( -4;1 \right)\) và \(C\left( -1;-1 \right)\). Khẳng định nào dưới đây là đúng?
A. \(\overrightarrow{AB}=2\overrightarrow{AC}\).
B. \(\overrightarrow{AB}=\frac{1}{2}\overrightarrow{AC}\).
C. \(\overrightarrow{AB}=-2\overrightarrow{AC}\)
D. \(\overrightarrow{AB}=-\frac{1}{2}\overrightarrow{AC}\).
Câu 22. Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng \(d:\left\{ \begin{array}{*{35}{l}} x=-2-t \\ y=4+3t \\ \end{array} \right.\) Trong các vectơ sau, vectơ nào là vectơ chỉ phương của \(d\) ?
A. \(\vec{u}=\left( -2;4 \right)\).
B. \(\vec{v}=\left( 3;1 \right)\).
C. \(\vec{m}=\left( -1;-3 \right)\).
D. \(\vec{n}=\left( -1;3 \right)\).
Câu 23. Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng \(\text{ }\!\!\Delta\!\!\text{ }:x-3y-2=0\). Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của \(\text{ }\!\!\Delta\!\!\text{ }\) ?
A. \(\vec{u}=\left( -3;1 \right)\).
B. \(\vec{v}=\left( 3;1 \right)\).
C. \(\vec{m}=\left( -1;-3 \right)\).
D. \(\vec{n}=\left( 1;-3 \right)\).
Câu 24. Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng \(\text{ }\!\!\Delta\!\!\text{ }:-x+2y-2=0\). Trong các vectơ sau, vectơ nào là vectơ chỉ phương của \(\text{ }\!\!\Delta\!\!\text{ }\) ?
A. \(\vec{u}=\left( -1;2 \right)\).
B. \(\vec{v}=\left( -2;-1 \right)\).
C. \(\vec{m}=\left( -2;1 \right)\).
D. \(\vec{n}=\left( 1;2 \right)\).
Câu 25. Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng \(d:\left\{ \begin{array}{*{35}{l}} x=-2t \\ y=4+t. \\ \end{array} \right.\) Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của \(d\) ?
A. \(\vec{u}=\left( -2;1 \right)\).
B. \(\vec{v}=\left( 2;-1 \right)\).
C. \(\vec{m}=\left( 1;-2 \right)\).
D. \(\vec{n}=\left( 1;2 \right)\).
Câu 26. Đường thẳng đi qua \(A\left( -3;2 \right)\) và nhận \(\vec{n}=\left( 1;5 \right)\) làm vectơ pháp tuyến có phương trình tổng quát là:
A. \(x+5y+7=0\).
B. \(-x+5y-13=0\).
C. \(-5x+y-17=0\).
D. \(x+5y-7=0\).
Câu 27. Phương trình tham số của đường thẳng \(d\) đi qua \(A\left( 0;-2 \right)\) và có vectơ chỉ phương \(\vec{u}=\left( 2;-3 \right)\) là:
A. \(\left\{ \begin{array}{*{35}{l}} x=2t \\ y=-2-3t \\ \end{array} \right.\)
B. \(\left\{ \begin{array}{*{35}{l}} x=2 \\ y=-3-2t \\ \end{array} \right.\)
C. \(\left\{ \begin{array}{*{35}{l}} x=3t \\ y=3+2t \\ \end{array} \right.\)
D. \(\left\{ \begin{array}{*{35}{l}} x=2+t \\ y=-3-2t \\ \end{array} \right.\)
---(Để xem tiếp nội dung của đề thi các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
B. Đáp án
|
1A |
2C |
3B |
4A |
5A |
6C |
7D |
8C |
9C |
10B |
11D |
12C |
13B |
14B |
15B |
16D |
17B |
18A |
|
19C |
20A |
21A |
22D |
23D |
24B |
25D |
26D |
27A |
28C |
29B |
30B |
31D |
32C |
33C |
34B |
35C |
|
Trên đây là một phần trích đoạn nội dung Đề thi giữa HK2 môn Toán 10 KNTT năm 2022-2023 Trường THPT Lê Quý Đôn có đáp án. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Mời các em tham khảo tài liệu có liên quan:
- Đề thi giữa HK2 môn Toán 10 CTST năm 2022-2023 Trường THPT Trần Hưng Đạo có đáp án
- Bộ 5 đề thi giữa HK2 môn Ngữ văn 10 Cánh diều năm 2022-2023 có đáp án trường THPT Đinh Tiên Hoàng
Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.
Tài liệu liên quan
Tư liệu nổi bật tuần
-
Đề thi minh họa môn Hóa học tốt nghiệp THPT năm 2025
22/10/20241740 -
Đề thi minh họa môn Tin học tốt nghiệp THPT năm 2025
22/10/2024690 -
Đề thi minh họa môn Toán tốt nghiệp THPT năm 2025
22/10/20241300 - Xem thêm





