Bài tập 6 trang 99 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Số đo của cung lớn bằng hiệu giữa \(360^o\) và số đo cung nhỏ(có chung hia mút với cung lớn).

+) Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

+) Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.

+) Hai cung được là bằng nhau nếu chúng có số đo bằng nhau.

+) Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.

Lời giải chi tiết

a) Trong (O; R) ta có: \(\widehat {AOB}\) = sđ cung AB (nhỏ)

Trong (O’; R) ta có: \(\widehat {AO'B}\) = sđ cung AB (nhỏ)

Vì số đo cung AB nhỏ của (O; R) lớn hơn số đo cung AB nhỏ của (O’; R’)

Suy ra: \(\widehat {AOB} > \widehat {AO'B}\)                   (1)

\(\Delta AOO' = \Delta BOO'\) (cạnh – cạnh – cạnh)

\( \Rightarrow \widehat {AOO'} = \widehat {BOO'} = {1 \over 2}\widehat {AOB}\)          (2)

\(\widehat {AO'O} = \widehat {BO'O} = {1 \over 2}\widehat {AO'B}\)           (3)

Từ (1), (2) và (3) suy ra: \(\widehat {AOO'} > \widehat {AO'O}\)

Trong \(\Delta AOO'\) ta có:  \(\widehat {AOO'} > \widehat {AO'O}\)

Suy ra: O’A > OA hay R’ > R

Trường hợp hình thứ 2, ta lấy đối xứng của (O) qua trục AB ta có kết quả như hình trên.

 

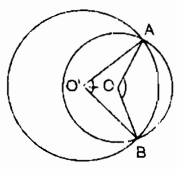
b) Trong (O; R) số đo cung lớn AB cộng với số đo cung nhỏ AB bằng 360⁰

Mà số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’; R’)

Suy ra số đo cung nhỏ AB của (O; R) lớn hơn số đo cung nhỏ của (O’; R’)

Chứng minh tương tự câu a ta có: R > R’.

c) Số đo hai cung nhỏ của (O; R) và (O’; R’) bằng nhau

\( \Rightarrow \widehat {AOB} = \widehat {AO'B}\)

Suy ra: \(\widehat {AOO'} = \widehat {AO'O} \Rightarrow \Delta AOO'\) cân tại A nên OA = OA’ hay R = R’.

-- Mod Toán 9 HỌC247