Bài tập 4 trang 99 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

+) Nếu một đường thẳng là tiếp điểm của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

Lời giải chi tiết

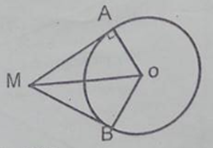
Xét đường trong \((O)\) có: \(MA \bot OA\) (tính chất tiếp tuyến)

Trong \(∆MAO\) có \(\widehat {OAM} = {90^0},\) ta có:

\(\cos\widehat {AOM} = \displaystyle{{OA} \over {OM}} = {R \over {2R}} = {1 \over 2}\)

\( \Rightarrow \widehat {AOM} = {60^0}\)

Lại có \(OM\) là tia phân giác của góc \(AOB\) (tính chất \(2\) tiếp tuyến MA, MB cắt nhau nhau tại M)

Suy ra \(\widehat {AOM} =  \displaystyle{1 \over 2}\widehat {AOB}\) 

\( \Rightarrow \widehat {AOB} = 2\widehat {AOM} = {120^0}\)

-- Mod Toán 9 HỌC247