Giải bài 55 tr 165 sách BT Toán lớp 9 Tập 1
Cho đường tròn \((O; 2cm),\) các tiếp tuyến \(AB\) và \(AC\) kẻ từ \(A\) đến đường tròn vuông góc với nhau tại \(A\) \((B\) và \(C\) là các tiếp điểm\().\)
\(a)\) Tứ giác \(ABOC\) là hình gì\(?\) Vì sao\(?\)
\(b)\) Gọi \(M\) là điểm bất kì thuộc cung nhỏ \(BC.\) Qua \(M\) kẻ tiếp tuyến với đường tròn, cắt \(AB\) và \(AC\) theo thứ tự tại \(D\) và \(E.\) Tính chu vi tam giác \(ADE.\)
\(c)\) Tính số đo góc \(DOE.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
\(*\)) Tứ giác có ba góc vuông là hình chữ nhật.
\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
\(*\)) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Lời giải chi tiết
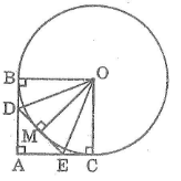
\(a)\) Ta có: \(AB ⊥ AC \Rightarrow \widehat {BAC} = 90^\circ \)
\(AB ⊥ BO \Rightarrow \widehat {ABO} = 90^\circ \)
\( AC ⊥ CO \Rightarrow \widehat {ACO} = 90^\circ \)
Tứ giác \(ABOC\) có \(3\) góc vuông nên nó là hình chữ nhật.
Mặt khác: \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra tứ giác \(ABOC\) là hình vuông.
\(b)\) Theo tính chất hai tiếp tuyến cắt nhau ta có:
\( DB = DM\)
\( EM = EC\)
Chu vi của tam giác \(ADE\) bằng:
\(AD + DE + EA \)\(= AD + DM + ME + EA\)
\( = AD + DB + AE + EC\)
\( = AB + AC = 2AB\)
Mà tứ giác \(ABOC\) là hình vuông (chứng minh trên) nên:
\(AB = OB = 2 (cm)\)
Vậy chu vi của tam giác \(ADE\) bằng: \(2.2 = 4 (cm)\)
\(c)\) Theo tính chất hai tiếp tuyến cắt nhau ta có:
+ \(OD\) là tia phân giác của góc \(BOM\)
Suy ra: \(\widehat {BOD} = \widehat {DOM} =\displaystyle {1 \over 2}\widehat {BOM}\)
+ \( OE\) là tia phân giác của góc \(COM\)
Suy ra: \(\widehat {COE} = \widehat {EOM} = \displaystyle {1 \over 2}\widehat {COM}\)
Suy ra:
\(\widehat {DOE} = \widehat {DOM} + \widehat {EOM} \)
\(= \displaystyle {1 \over 2}(\widehat {BOM} + \widehat {COM})\)
\(= \displaystyle {1 \over 2}\widehat {COB} = {1 \over 2}.90^\circ = 45^\circ \).
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 53 trang 165 SBT Toán 9 Tập 1
Bài tập 54 trang 165 SBT Toán 9 Tập 1
Bài tập 56 trang 165 SBT Toán 9 Tập 1
Bài tập 57 trang 165 SBT Toán 9 Tập 1
Bài tập 58 trang 165 SBT Toán 9 Tập 1
Bài tập 59 trang 165 SBT Toán 9 Tập 1
Bài tập 60 trang 166 SBT Toán 9 Tập 1
Bài tập 61 trang 166 SBT Toán 9 Tập 1
Bài tập 62 trang 166 SBT Toán 9 Tập 1
Bài tập 63 trang 166 SBT Toán 9 Tập 1
Bài tập 6.1 trang 166 SBT Toán 9 Tập 1
-


Chứng minh EF là tiếp tuyến của đường tròn đường kính BH
bởi Goc pho
 26/01/2019
26/01/2019
Cho nửa đường tròn (O) đường kính BC và điểm A nằm trong nửa đường tròn (A\(\ne\) B,C). Kẻ AH\(\perp\)BC (H\(\in\)BC). Trên nửa mặt phẳng bờ BC chứa A vẽ 2 nửa đường tròn , đường kính HB và HC. Chúng cắt AB và AC ở E và F.
a, Chứng Minh: AE.AB=AF.AC
b, Chứng Minh: EF là tiếp tuyến của đường tròn đường kính BH
c, Gọi I và K là 2 điểm của H qua AB và AC. Chứng Minh I,A,K thẳng hàng.
d, IK cắt tiếp tuyến kẻ từ B của (O) tại M. Chứng Minh: MC,AH,EF đồng qui.
- Mọi người ơi giúp em với ! EM Cảm Ơn Nhiều Ạ !
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tam giác AMB là tam giác đều
bởi Nhat nheo
 26/01/2019
26/01/2019
Cho đường tròn (O; 5cm) điểm M nằm bên ngoài đường tròn. Kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Biết góc AMB bằng 600.
a) CMR: tam giác AMB là tam giác đều
b) Tính chu vi tam giác AMB
c) Tia AO cắt đường tròn ở C. Tứ giác BMOC là hình gì? Vì sao?
Theo dõi (0) 1 Trả lời -


Chứng minh I cách đều AV, BC, AC
bởi Trần Phương Khanh
 26/01/2019
26/01/2019
Cho A nằm ngoài (O). Vẽ tiếp tuyến AB,AC tới (O). Kéo CD là đg kính. AO cắt (O) tại I. Chứng minh I cách đều AV,BC,AC
Theo dõi (0) 1 Trả lời





