Bài tập 57 trang 165 SBT Toán 9 Tập 1
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức: S = p.r
Hướng dẫn giải chi tiết
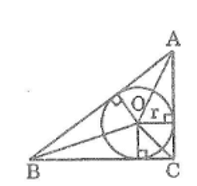
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : SABC = SOAB + SOAC + SOBC
= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r
= (1/2)(AB + AC + BC).r
Mà AB + AC + BC = 2p
Nên SABC =(1/2).2p.r = p.r
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 55 trang 165 SBT Toán 9 Tập 1
Bài tập 56 trang 165 SBT Toán 9 Tập 1
Bài tập 58 trang 165 SBT Toán 9 Tập 1
Bài tập 59 trang 165 SBT Toán 9 Tập 1
Bài tập 60 trang 166 SBT Toán 9 Tập 1
Bài tập 61 trang 166 SBT Toán 9 Tập 1
Bài tập 62 trang 166 SBT Toán 9 Tập 1
Bài tập 63 trang 166 SBT Toán 9 Tập 1
Bài tập 6.1 trang 166 SBT Toán 9 Tập 1
-


Bài 63 trang 166 sách bài tập toán 9 tập 1
bởi Thùy Trang
 10/10/2018
Bài 63* (Sách bài tập - tập 1 - trang 166)
10/10/2018
Bài 63* (Sách bài tập - tập 1 - trang 166)Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh rằng :
\(S_{ABC}=BD.DC\)
Theo dõi (0) 1 Trả lời -


Bài 62* trang 166 sách bài tập toán 9 tập 1
bởi Phạm Khánh Linh
 10/10/2018
Bài 62* (Sách bài tập - tập 1 - trang 166)
10/10/2018
Bài 62* (Sách bài tập - tập 1 - trang 166)Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua một điểm M thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt Ax, By theo thứ tự ở C, D. Gọi N là giao điểm của AD và BC, H là giao điểm của MN và AB. Chứng minh rằng :
a) \(MN\perp AB\)
b) \(MN=NH\)
Theo dõi (0) 1 Trả lời -


Bài 61* trang 166 sách bài tập toán 9 tập 1
bởi Bánh Mì
 10/10/2018
Bài 61* (Sách bài tập - tập 1 - trang 166)
10/10/2018
Bài 61* (Sách bài tập - tập 1 - trang 166)Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C, D
a) Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB
b) Tìm vị trí của điểm M để hình thang ABCD có chu vi nhỏ nhất
c) Tìm vị trí của C, D để hình thang ABDC có chu vi bằng 14 cm, biết AB = 4cm
Theo dõi (0) 1 Trả lời