Giải bài 47 tr 59 sách BT Toán lớp 9 Tập 2
Giải các phương trình sau bằng cách đưa về phương trình tích:
a) \(3{x^2} + 6{x^2} - 4x = 0\)
b) \({\left( {x + 1} \right)^3} - x + 1 = \left( {x - 1} \right)\left( {x - 2} \right)\)
c) \({\left( {{x^2} + x + 1} \right)^2} = {\left( {4x - 1} \right)^2}\)
d) \({\left( {{x^2} + 3x + 2} \right)^2} = 6\left( {{x^2} + 3x + 2} \right)\)
e) \({\left( {2{x^2} + 3} \right)^2} - 10{x^3} - 15x = 0\)
f) \({x^3} - 5{x^2} - x + 5 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
* Chuyển tất cả các hạng tử về vế trái, sau đó đặt nhân tử chung để đưa phương trình về dạng phương trình tích.
\(\begin{array}{l}
A\left( x \right).B\left( x \right).C\left( x \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
A\left( x \right) = 0\\
B\left( x \right) = 0\\
C\left( x \right) = 0
\end{array} \right.
\end{array}\)
* Phương trình \(a{x^2} + bx + c = 0\;(a \ne 0)\) và biệt thức \(\Delta' = {b'^2} - ac\):
+) Nếu \(\Delta' > 0\) thì phương trình có hai nghiệm phân biệt:
\({x_1}\)= \(\dfrac{-b' + \sqrt{\bigtriangleup' }}{a}\) và \({x_2}\)= \(\dfrac{-b' - \sqrt{\bigtriangleup' }}{a}\)
+) Nếu \(\Delta' = 0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b' }{a}\).
+) Nếu \(\Delta' < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết
Giải các phương trình sau bằng cách đưa về phương trình tích.
a) \(3{x^3} + 6{x^2} - 4x = 0 \Leftrightarrow x\left( {3{x^2} + 6x - 4} \right) = 0\)
x = 0 hoặc \(3{x^2} + 6x - 4 = 0\)
\(\eqalign{
& 3{x^2} + 6x - 4 = 0 \cr
& \Delta ' = {3^2} - 3.\left( { - 4} \right) = 9 + 12 = 21 > 0 \cr
& \sqrt {\Delta '} = \sqrt {21} \cr
& {x_1} = {{ - 3 + \sqrt {21} } \over 3};{x_2} = {{ - 3 - \sqrt {21} } \over 3} \cr} \)
Vậy phương trình có 3 nghiệm: \({x_1} = 0;{x_2} = {{ - 3 + \sqrt {21} } \over 3};{x_3} = {{ - 3 - \sqrt {21} } \over 3}\)
b)
\(\eqalign{
& {\left( {x + 1} \right)^3} - x + 1 = \left( {x - 1} \right)\left( {x - 2} \right) \cr
& \Leftrightarrow {x^3} + 3{x^2} + 3x + 1 - x + 1 = {x^2} - 2x - x + 2 \cr
& \Leftrightarrow {x^3} + 2{x^2} + 5x = 0 \cr
& \Leftrightarrow x\left( {{x^2} + 2x + 5} \right) = 0 \cr} \)
x = 0 hoặc \({x^2} + 2x + 5 = 0\)
\(\eqalign{
& {x^2} + 2x + 5 = 0 \cr
& \Delta ' = 1 - 1.5 = 1 - 5 = - 4 < 0 \cr} \)
Phương trình vô nghiệm.
Vậy phương trình đã cho có một nghiệm x = 0
c)
\(\eqalign{
& {\left( {{x^2} + x + 1} \right)^2} = {\left( {4x - 1} \right)^2} \cr
& \Leftrightarrow {\left( {{x^2} + x + 1} \right)^2} - {\left( {4x - 1} \right)^2} = 0 \cr
& \Leftrightarrow \left[ {\left( {{x^2} + x + 1} \right) + \left( {4x - 1} \right)} \right]\left[ {\left( {{x^2} + x + 1} \right) - \left( {4x - 1} \right)} \right] = 0 \cr
& \Leftrightarrow \left( {{x^2} + x + 1 + 4x - 1} \right)\left( {{x^2} + x + 1 - 4x + 1} \right) = 0 \cr
& \Leftrightarrow \left( {{x^2} + 5x} \right)\left( {{x^2} - 3x + 2} \right) = 0 \cr
& \Leftrightarrow x\left( {x + 5} \right)\left( {{x^2} - 3x + 2} \right) = 0 \cr
& \Leftrightarrow \left[ {\matrix{
{x = 0} \cr
{x + 5 = 0} \cr
{{x^2} - 3x + 2 = 0} \cr} } \right. \cr} \)
x + 5 = 0 ⇒ x = -5
\({x^2} - 3x + 2 = 0\) có dạng: \(a + b + c = 0\), ta có: \(1 + \left( { - 3} \right) + 2 = 0\)
\({x_1} = 1;{x_2} = 2\)
Vậy phương trình đã cho có 4 nghiệm: \({x_1} = 0;{x_2} = - 5;{x_3} = 1;{x_4} = 2\)
d)
\(\eqalign{
& {\left( {{x^2} + 3x + 2} \right)^2} = 6\left( {{x^2} + 3x + 2} \right) \cr
& \Leftrightarrow {\left( {{x^2} + 3x + 2} \right)^2} - 6\left( {{x^2} + 3x + 2} \right) = 0 \cr
& \Leftrightarrow \left( {{x^2} + 3x + 2} \right)\left[ {\left( {{x^2} + 3x + 2} \right) - 6} \right] = 0 \cr
& \Leftrightarrow \left( {{x^2} + 3x + 2} \right)\left( {{x^2} + 3x - 4} \right) = 0 \cr
& \Leftrightarrow \left[ {\matrix{
{{x^2} + 3x + 2 = 0} \cr
{{x^2} + 3x - 4 = 0} \cr} } \right. \cr} \)
\({x^2} + 3x + 2 = 0\) có dạng: \(a - b + c = 0\), ta có:
\(\eqalign{
& 1 - 3 + 2 = 0 \cr
& {x_1} = - 1;{x_2} = - 2 \cr} \)
\({x^2} + 3x - 4 = 0\) có dạng: $a + b + c = 0\)
\(\eqalign{
& 1 + 3 + \left( { - 4} \right) = 0 \cr
& {x_3} = 1;{x_4} = - 4 \cr} \)
Vậy phương trình đã cho có 4 nghiệm: \({x_1} = - 1;{x_2} = - 2;{x_3} = 1;{x_4} = - 4\)
e)
\(\eqalign{
& {\left( {2{x^2} + 3} \right)^2} - 10{x^3} - 15x = 0 \cr
& \Leftrightarrow {\left( {2{x^2} + 3} \right)^2} - 5x\left( {2{x^2} + 3} \right) = 0 \cr
& \Leftrightarrow \left( {2{x^2} + 3} \right)\left( {2{x^2} + 3 - 5x} \right) = 0 \cr} \)
Ta có:
\(\eqalign{
& 2{x^2} \ge 0 \Rightarrow 2{x^2} + 3 > 0 \cr
& \Rightarrow 2{x^2} - 5x + 3 = 0 \cr} \)
Phương trình có dạng: \(a + b + c = 0\)
Ta có:
\(\eqalign{
& 2 + \left( { - 5} \right) + 3 = 0 \cr
& {x_1} = 1;{x_2} = {3 \over 2} \cr} \)
Vậy phương trình đã cho có 2 nghiệm: \({x_1} = 1;{x_2} = {3 \over 2}\)
f)
\(\eqalign{
& {x^3} - 5{x^2} - x + 5 = 0 \cr
& \Leftrightarrow {x^2}\left( {x - 5} \right) - \left( {x - 5} \right) = 0 \cr
& \Leftrightarrow \left( {x - 5} \right)\left( {{x^2} - 1} \right) = 0 \cr
& \Leftrightarrow \left( {x - 5} \right)\left( {x - 1} \right)\left( {x + 1} \right) = 0 \cr
& \left[ {\matrix{
{x - 5 = 0} \cr
{x + 1 = 0} \cr
{x - 1 = 0} \cr} \Leftrightarrow \left[ {\matrix{
{x = 5} \cr
{x = - 1} \cr
{x = 1} \cr} } \right.} \right. \cr} \)
Vậy phương trình đã cho có 3 nghiệm: \({x_1} = 5;{x_2} = - 1;{x_3} = 1\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình trùng phương: \(4x^4 + x^2– 5 = 0\)
bởi Bánh Mì
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phường trình: 2x(x-3)=7-x
bởi Nguyễn Dự
 26/01/2021
Giải hpt
26/01/2021
Giải hpt Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


A. 0
B. 1
C. 2
D. 4
Theo dõi (0) 1 Trả lời -
ADMICRO


Giải phương trình: \(2{x^3} - {x^2} + 3x + 6 = 0\)
bởi Phan Quân
 21/01/2021
Theo dõi (0) 1 Trả lời
21/01/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình \(8x^2 - x - 3x(2x-3) = -x(x-2)\)?
bởi Trần Ngọc
 13/08/2020
Theo dõi (0) 0 Trả lời
13/08/2020
Theo dõi (0) 0 Trả lời -


Giải pt: \(x^4 + 9x^2 = 0\)?
bởi Vũ Thị Trang
 28/06/2020
28/06/2020
Giúp mình ý 1 câu 1 với ạ
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng tỏ phương trình luôn có nghiệm với mọi x?
bởi Mỹ Dung Dung
 11/06/2020
11/06/2020
Bài 1:Cho phương trình
\(x^2-2mx-4m-4=0 \)(m là tham số)
a,Giải phương trình khi m=1
b,Chứng tỏ phương trình luôn có nghiệm với mọi x?
Theo dõi (0) 2 Trả lời -


Giải phương trình khi m=2?
bởi Trần Quang
 25/05/2020
25/05/2020
Giúp mk vs ạ
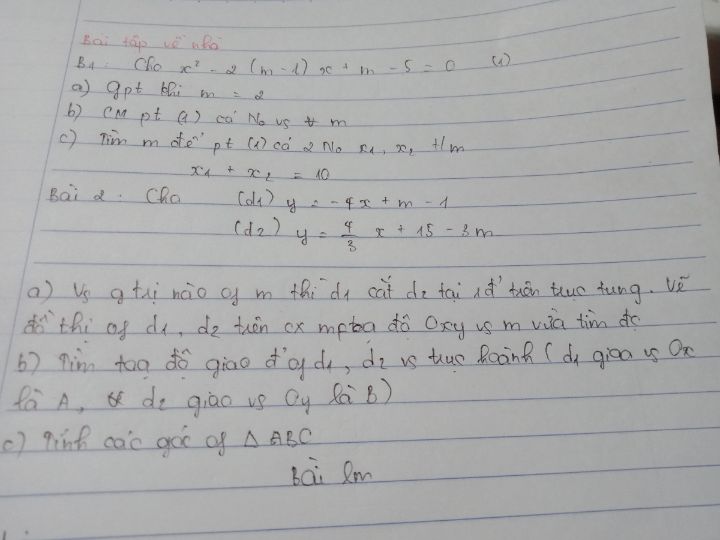 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tìm m để ba đường thẳng cắt nhau tại 1 điểm?
bởi đỗ quỳnh anh
 20/05/2020
20/05/2020
Giúp mih bài 3 ạ
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm m để phương trình x^4-3x^2+m-1=0 có đúng 3 nghiệm
bởi An An
 19/05/2020
19/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm x biết 2x:x+1=x2-x 8:(x+1)*(x-4)
bởi Đỗ Thu Hiền
 10/05/2020
Ai giải hộ câu này với ạ
10/05/2020
Ai giải hộ câu này với ạ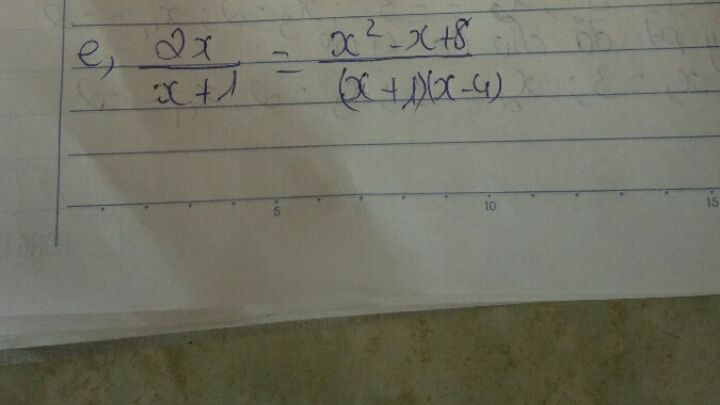 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời -


Tìm GTLN của I=-x^2+2x-3
bởi Duẩn Nguyễn
 27/04/2020
27/04/2020
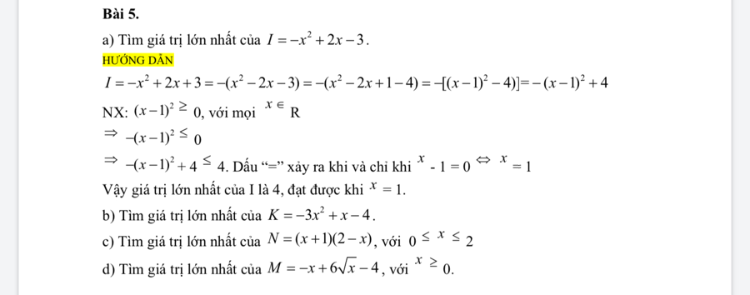 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (x+5)(x+6)(x+8)(x+9)=0
bởi Nguyễn Quỳnh
 21/04/2020
21/04/2020
Giải phương trình (x+5)(x+6)(x+8)(x+9)=0
Theo dõi (0) 2 Trả lời -


Giải phương trình x*4-x*3-3x*2-3x+3=0
bởi Jack Ky
 20/04/2020
20/04/2020
X*4-x*3-3x*2-3x+3=0
Theo dõi (0) 0 Trả lời






