Giải bài 36 tr 57 sách BT Toán lớp 9 Tập 2
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình:
a) \(2{x^2} - 7x + 2 = 0\)
b) \(2{x^2} + 9x + 7 = 0\)
c) \(\left( {2 - \sqrt 3 } \right){x^2} + 4x + 2 + \sqrt 2 = 0\)
d) \(1,4{x^2} - 3x + 1,2 = 0\)
e) \(5{x^2} + x + 2 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Nếu \({x_1},{\rm{ }}{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) thì:
\(\left\{\begin{matrix} x_{1} + x_{2} = -\dfrac{b}{a}& & \\ x_{1}x_{2}=\dfrac{c}{a} & & \end{matrix}\right.\)
Lời giải chi tiết
a)
\(\eqalign{
& 2{x^2} - 7x + 2 = 0 \cr
& \Delta = {\left( { - 7} \right)^2} - 4.2.2 = 49 - 16 = 33 > 0 \cr} \)
Phương trình có hai nghiệm phân biệt.
Theo hệ thức Vi-ét ta có:
\({x_1} + {x_2} = {7 \over 2};{x_1}{x_2} = {2 \over 2} = 1\)
b)
\(\eqalign{
& 5{x^2} + 2x - 16 = 0 \cr
& a = 5;c = - 16;ac < 0 \cr} \)
Phương trình có hai nghiệm phân biệt.
Theo hệ thức Vi-ét ta có:
\({x_1} + {x_2} = - {2 \over 5};{x_1}{x_2} = - {{16} \over 5}\)
c)
\(\eqalign{
& \left( {2 - \sqrt 3 } \right){x^2} + 4x + 2 + \sqrt 2 = 0 \cr
& \Delta ' = {2^2} - \left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 2 } \right) = 4 - 4 - 2\sqrt 2 + 2\sqrt 3 + \sqrt 6 \cr
& = 2\sqrt 3 + \sqrt 6 - 2\sqrt 2 > 0 \cr} \)
Phương trình có hai nghiệm phân biệt.
Theo hệ thức Vi-ét ta có:
\(\eqalign{
& {x_1} + {x_2} = {{ - 4} \over {2 - \sqrt 3 }} = - 4\left( {2 + \sqrt 3 } \right) \cr
& {x_1}{x_2} = {{2 + \sqrt 2 } \over {2 - \sqrt 3 }} = {{\left( {2 + \sqrt 2 } \right)\left( {2 + \sqrt 3 } \right)} \over {4 - 3}} = 4 + 2\sqrt 3 + 2\sqrt 2 + \sqrt 6 \cr} \)
d)
\(\eqalign{
& 1,4{x^2} - 3x + 1,2 = 0 \cr
& \Delta = {\left( { - 3} \right)^2} - 4.1,4.1,2 = 9 - 6,72 = 2,28 > 0 \cr} \)
Phương trình có hai nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
\(\eqalign{
& {x_1} + {x_2} = - {{ - 3} \over {1,4}} = {{30} \over {14}} = {{15} \over 7} \cr
& {x_1}{x_2} = {{1,2} \over {1,4}} = {6 \over 7} \cr} \)
e)
\(\eqalign{
& 5{x^2} + x + 2 = 0 \cr
& \Delta = 1 - 4.5.2 = 1 - 40 = - 39 < 0 \cr} \)
Phương trình vô nghiệm, không có tổng và tích của các nghiệm.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 33 trang 54 SGK Toán 9 Tập 2
Bài tập 35 trang 57 SBT Toán 9 Tập 2
Bài tập 37 trang 57 SBT Toán 9 Tập 2
Bài tập 38 trang 57 SBT Toán 9 Tập 2
Bài tập 39 trang 57 SBT Toán 9 Tập 2
Bài tập 40 trang 57 SBT Toán 9 Tập 2
Bài tập 41 trang 58 SBT Toán 9 Tập 2
Bài tập 42 trang 58 SBT Toán 9 Tập 2
Bài tập 43 trang 58 SBT Toán 9 Tập 2
Bài tập 44 trang 58 SBT Toán 9 Tập 2
Bài tập 6.1 trang 58 SBT Toán 9 Tập 2
Bài tập 6.1 trang 58 SBT Toán 9 Tập 2
-


Giải hộ e bài tập 1 câu 2
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Hãy tính giá trị biểu thức sau bằng \({x_1} + {x_2};\,\,P = {x_1}.{x_2};\,\,M = {x_1}^2 + {x_2}^2;\,\,N = \left| {{x_1} - {x_2}} \right|\)? Với \({x_1} , {x_2}\) là nghiệm của phương trình \(3x^2+9x-1=0\)?
bởi hshs shshs
 12/06/2020
12/06/2020
gọi x1, x2 là nghiệm của phương trình \(3x^2+9x-1=0\)?. Hãy tính giá trị biểu thức sau bằng \({x_1} + {x_2};\,\,P = {x_1}.{x_2};\,\,M = {x_1}^2 + {x_2}^2;\,\,N = \left| {{x_1} - {x_2}} \right|\)
Theo dõi (0) 1 Trả lời -


Tìm m để phương trình có 2 nghiệm trái dấu?
bởi Hương Nguyễn
 10/06/2020
10/06/2020
Giúp mk vs ạ
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm m để phương trình có 2 nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(x_1=x_2^2\)?
bởi Cao Thi Linh Thu
 09/06/2020
09/06/2020
Giải bài tập toán
Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + 2m - 3 = 0\).Tìm m để phương trình có 2 nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(x_1=x_2^2\)?
Theo dõi (0) 1 Trả lời -
ADMICRO


Tìm giá trj của m để phương trình \(x^2+2x+m-1=0\) có hai nghiệm phân biệt thỏa mãn \(x_1^3 + x_2^3 - 6{x_1}{x_2} = 4\left( {m - {m^2}} \right)\)?
bởi Nhan Bui
 09/06/2020
09/06/2020
Làm hộ câu 2 đề thi tuyển sinh năm 2019 môn toán của tỉnh Quảng Ninh nha
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm m để phương trình \({x^2} - 4x + {m^2} + 3 = 0\) có hai nhiệm phân biệt thỏa mãn \({x_2} = 5{x_1}.\)?
bởi Jihyeon Won
 07/06/2020
07/06/2020
Cho pt x²-4x-m² 3=0Tìm m để ̉pt có 2 nghiệm x1,x2 thỏa mãn x2=5x1.
Theo dõi (0) 1 Trả lời -


Tìm nghiệm còn lại?
bởi Nguyễn Thu Thảo
 06/06/2020
06/06/2020
Giải giúp mình với
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Xác định m để PT có hai nghiệm phân biệt \(x_1; x_2\) thỏa mãn \(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{7}{4}\)?
bởi Thành Duy
 05/06/2020
05/06/2020
Giúp e bài 10
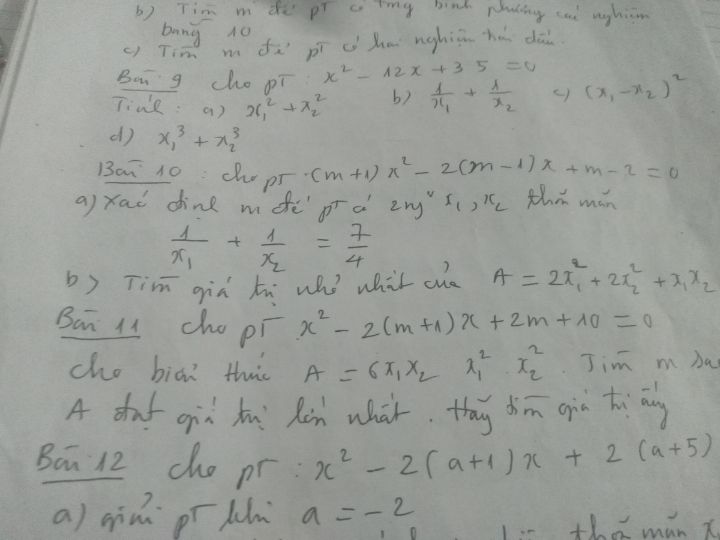 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Xác định m để phương trình có hai nghiệm trái dấu?
bởi Yi Yi
 04/06/2020
Cho phương trình (m-1)x^2 -5x 2=0 ( x là ẩn m là tham số) . a) xác định giá trị của m để phương trình có 2 nghiệm trái dấuTheo dõi (0) 1 Trả lời
04/06/2020
Cho phương trình (m-1)x^2 -5x 2=0 ( x là ẩn m là tham số) . a) xác định giá trị của m để phương trình có 2 nghiệm trái dấuTheo dõi (0) 1 Trả lời -


Tìm u và v biết u + v = 23 và u, v = 231?
bởi Hiếu Chu Văn
 24/05/2020
24/05/2020
Tìm u và v trong mỗi trường hợp sau :
a) u+ v=23 , uv=231.
b) u+ v=-8 , uv=-105
c) u +v=2 , uv=9
LÀM NHƯ THẾ NÀO MỌI NGƯỜI ƠI GIÚP TÔI ƠI THANK YOU !!!!!!!!!!!!!!!!!!!!!!
Theo dõi (0) 0 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm m để phương trình x^2+3x+3m+5=0 có 2 nghiệm
bởi Đỗ Thu Hiền
 14/05/2020
Giúp mình bài này với nha
14/05/2020
Giúp mình bài này với nha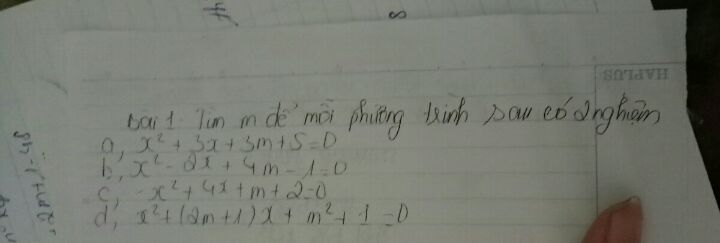 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Giải phương trình (x-2)^2=(2x-4)(5-x)
bởi Phương Cẩm
 13/05/2020
13/05/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -

 Bài 2 ạ
Bài 2 ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình x^2 -5x+m+4 = 0 có 2 nghiệm x1, x2 thoả mãn 3x1+4x2 = 6
bởi Phạm Thảo
 09/05/2020
09/05/2020
Cho phương trình x^2 -5x+m+4 = 0 Tìm m để phương trình có 2 nghiệm x1,x2 thoả mãn 3x1+4x2 = 6
Theo dõi (0) 2 Trả lời -

 Tìm tất cả các giá trị để pt có nghiệm . Gọi x1x2 là 2nghieemj của ptTheo dõi (1) 3 Trả lời
Tìm tất cả các giá trị để pt có nghiệm . Gọi x1x2 là 2nghieemj của ptTheo dõi (1) 3 Trả lời -


Tìm điều kiện của m để phương trình x^2 - 2(m-2)x + 2m - 5 = 0 có hai nghiệm phân biệt x1, x2
bởi Hồng Chinh
 03/05/2020
03/05/2020
Cho phương trình: x2 - 2(m-2)x + 2m - 5 = 0 ( m là tham số)
a. Tìm điều kiện của m để phương trình có hai nghiệm phân biệt x1, x2
b. Với m tìm được ở trên, tìm biểu thức liên hệ giữa x1, x2 không phụ thuộc vào m
Theo dõi (0) 1 Trả lời





