Phần hướng dẫn giải bài tập Hình học 8 Bài 1 Đa giác - Đa giác đều sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Hình học 8 Tập 1
-
Bài tập 1 trang 115 SGK Toán 8 Tập 1
Hãy vẽ một lục giác lồi. Hãy nêu cách nhận biết một lục giác lồi.
-
Bài tập 2 trang 115 SGK Toán 8 Tập 1
Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:
a) Có tất cả các cạnh bằng nhau;
b) Có tất cả các góc bằng nhau.
-
Bài tập 3 trang 115 SGK Toán 8 Tập 1
Cho hình thoi ABCD có \(\widehat{A}=60^0\) . Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
-
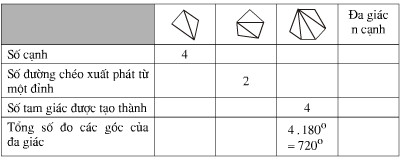
Bài tập 4 trang 115 SGK Toán 8 Tập 1
Điền số thích hợp vào các ô trống trong bảng
- VIDEOYOMEDIA
-
Bài tập 5 trang 115 SGK Toán 8 Tập 1
Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n- giác đều.
-
Bài tập 1 trang 155 SBT Toán 8 Tập 1
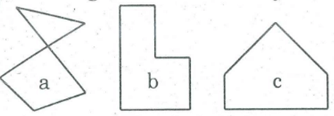
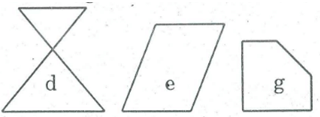
Trong các hình dưới đây hình nào là đa giác lồi? Vì sao?
-
Bài tập 2 trang 155 SBT Toán 8 Tập 1
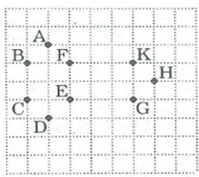
Hình vẽ bên. Hãy vẽ một đa giác lồi mà các đỉnh là một trong các điểm đã cho trong hình.
-
Bài tập 3 trang 155 SBT Toán 8 Tập 1
Cho ví dụ về các đa giác đều mà cạnh của chúng bằng nhau.
-
Bài tập 4 trang 156 SBT Toán 8 Tập 1
Chứng minh rằng số đo của một hình n-giác đều là \(\frac{{\left( {n - 2} \right){{.180}^0}}}{n}\)
-
Bài tập 5 trang 156 SBT Toán 8 Tập 1
Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.
-
Bài tập 6 trang 156 SBT Toán 8 Tập 1
a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác
b) Chứng minh rằng hình n-giác có tất cả \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
-
Bài tập 7 trang 15 SBT Toán 6 Tập 1
Tìm số đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh.
-
Bài tập 8 trang 156 SBT Toán 8 Tập 1
Chứng minh rằng tổng các góc ngoài của một đa giác có số đo bằng 3600.
-
Bài tập 9 trang 156 SBT Toán 8 Tập 1
Đa giác nào có tổng số đo các góc trong bằng tổng số đo các góc ngoài?
-
Bài tập 10 trang 156 SBT Toán 8 Tập 1
Đa giác có nhiều nhất là bao nhiêu góc nhọn?
-
Bài tập 11 trang 156 SBT Toán 8 Tập 1
Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác đó bằng 4680. Hỏi đa giác đều đó có mấy cạnh?
-
Bài tập 1.1 trang 156 SBT Toán 8 Tập 1
Mỗi câu sau đây đúng hay sai ?
a. Tam giác và tứ giác không phải là đa giác
b. Hình gồm n đoạn thẳng đôi một có một điểm chung được gọi là đa giác (với n là số tự nhiên lớn hơn 2)
c. Hình gồm n đoạn thẳng (n là số tự nhiên lớn hơn 2) trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng được gọi là đa giác.
d. Hình tạo bởi nhiều hình tam giác được gọi là đa giác
e. Đa giác luôn nằm trong nửa mặt phẳng cho trước được gọi là đa giác lồi
f. Đa giác luôn nằm trong nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh của nó được gọi là đa giác lồi
g. Hình gồm hai đa giác lồi cho trước là một đa giác lồi.
-
Bài tập 1.2 trang 156 SBT Toán 8 Tập 1
a) Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
b) Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
c) Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
-
Bài tập 1.3 trang 157 SBT Toán 8 Tập 1
Cho hình vuông ABCD có AB = 3cm
Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm
Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm
Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm
Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm
Chứng minh KLMN là hình vuông
-
Bài tập 1 trang 155 SBT Toán 8 Tập 1
Trong các hình dưới đây (h.180), hình nào là đa giác lồi? Vì sao?
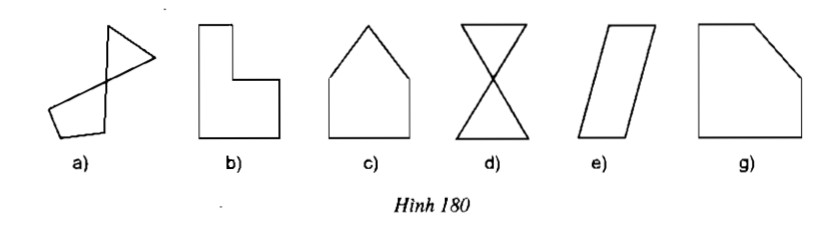
-
Bài tập 2 trang 155 SBT Toán 8 Tập 1
Hãy vẽ một đa giác (lồi) mà các đỉnh là một điểm trong các điểm đã cho ở hình 181 (trên lưới kẻ ô vuông).
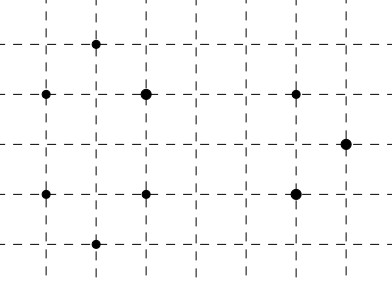
-
Bài tập 3 trang 155 SBT Toán 8 Tập 1
Em hãy kể tên một số đa giác đều mà em biết.
-
Bài tập 4 trang 156 SBT Toán 8 Tập 1
Chứng minh số đo góc của hình n- giác đều là \({{\left( {n - 2} \right){{.180}^0}} \over n}\)
-
Bài tập 5 trang 156 SBT Toán 8 Tập 1
Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.
-
Bài tập 6 trang 156 SBT Toán 8 Tập 1
a. Vẽ hình và tính ố đường chéo của ngũ giác, lục giác
b. Chứng minh rằng hình n – giác có tất cả \(({{n\left( {n - 3} \right)} \over 2}\) đường chéo.
-
Bài tập 7 trang 156 SBT Toán 8 Tập 1
Tìm ố đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh.
-
Bài tập 8 trang 156 SBT Toán 8 Tập 1
Chứng minh rằng tổng các góc ngoài của một đa giác (lồi ) có ố đo là 360°.
-
Bài tập 9 trang 156 SBT Toán 8 Tập 1
Đa giác nào có tổng số đo các góc (trong) bằng tổng số đo các góc ngoài?
-
Bài tập 10 trang 156 SBT Toán 8 Tập 1
Một đa giác (lồi) có nhiều nhất là bao nhiêu góc nhọn?
-
Bài tập 11 trang 156 SBT Toán 8 Tập 1
Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác bằng 468°. Hỏi đa giác đều đó có mấy cạnh ?
-
Bài tập 1.1 trang 156 SBT Toán 8 Tập 1
Mỗi câu sau đây đúng hay sai ?
a. Tam giác và tứ giác không phải là đa giác
b. Hình gồm \(n\) đoạn thẳng đôi một có một điểm chung được gọi là đa giác (với \(n\) là số tự nhiên lớn hơn \(2\))
c. Hình gồm \(n\) đoạn thẳng (với \(n\) là số tự nhiên lớn hơn \(2\)) trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng được gọi là đa giác.
d. Hình tạo bởi nhiều hình tam giác được gọi là đa giác
e. Đa giác luôn nằm trong nửa mặt phẳng cho trước được gọi là đa giác lồi
f. Đa giác luôn nằm trong nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh của nó được gọi là đa giác lồi
g. Hình gồm hai đa giác lồi cho trước là một đa giác lồi.
-
Bài tập 1.2 trang 156 SBT Toán 8 Tập 1
a. Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
b. Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
c. Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
-
Bài tập 1.3 trang 157 SBT Toán 8 Tập 1
Cho hình vuông ABCD có AB = 3cm
Trên tia đối của tia BA lấy điểm K ao cho BK = 1cm
Trên tia đối của tia CB lấy điểm L ao cho CL = 1cm
Trên tia đối của tia DC lấy điểm M ao cho MD = 1cm
Trên tia đối của tia AD lấy điểm N ao cho NA = 1cm
Chứng minh KLMN là hình vuông