Bài tập 1.2 trang 156 SBT Toán 8 Tập 1
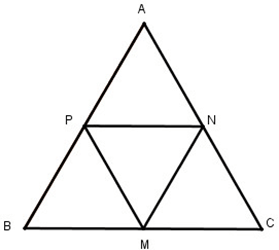
a) Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
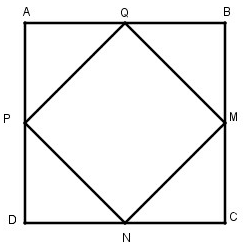
b) Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
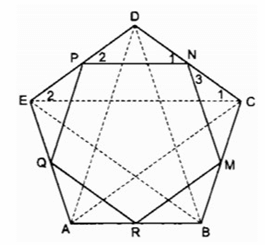
c) Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
Hướng dẫn giải chi tiết
a)
Ta có: M là trung điểm của BC
N là trung điểm của AC nên MN là đường trung bình của Δ ABC => MN = \(\frac{1}{2}\) AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của Δ ABC
=> MP = \(\frac{1}{2}\) AC
NP là đường trung bình của Δ ABC => NP = \(\frac{1}{2}\) BC
Mà AB = BC = AC (gt) => MN = MP = NP. Vậy Δ MNP đều
b)
Xét Δ APQ và Δ BQM:
AQ = BQ (gt)
\(\widehat A\) = \(\widehat B\) = 900
AP = BM (gt)
Do đó: Δ APQ = Δ BQM (c.g.c) => PQ = QM (1)
Xét Δ BQM và Δ CMN:
BM = CM (gt)
\(\widehat B\) = \(\widehat C\) = 900
BQ = CN (gt)
Do đó: Δ BQM = Δ CMN (c.g.c) => QM = MN (2)
Xét Δ CMN và Δ DNP:
CN = DN (gt)
\(\widehat C\) = \(\widehat D\) = 900
CM = DP (gt)
Do đó: Δ CMN = Δ DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên Δ APQ vuông cân tại A
BQ = BM nên Δ BMQ vuông cân tại B
=> \(\widehat AQP\) = \(\widehat BQM\) = 450
\(\widehat AQP\) + \(\widehat PQM\) + \(\widehat BQM\) = 1800 (kề bù)
=> \(\widehat PQM\) = 1800 - ( \(\widehat AQP\) + \(\widehat BQM\) )
= 1800- (450 + 450) = 900
Vậy tứ giác MNPQ là hình vuông.
c)
Xét Δ ABC và Δ BCD:
AB = BC (gt)
\(\widehat B\) = \(\widehat C\) (gt)
BC = CD (gt)
Do đó: Δ ABC = Δ BCD (c.g.c)
=> AC = BD (1)
Xét Δ BCD và Δ CDE:
BC = CD (gt)
\(\widehat C\) = \(\widehat D\) (gt)
CD = DE (gt)
Do đó: Δ BCD = Δ CDE (c.g.c) => BD = CE (2)
Xét Δ CDE và Δ DEA:
CD = DE (gt)
\(\widehat D\) = \(\widehat E\) (gt)
DE = EA (gt)
Do đó: Δ CDE = Δ DEA (c.g.c) => CE = DA (3)
Xét Δ DEA và Δ EAB:
DE = EA (gt)
\(\widehat D\) = \(\widehat A\) (gt)
EA = AB (gt)
Do đó: Δ DEA = Δ EAB (c.g.c) => DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong Δ ABC ta có RM là đường trung bình
=> RM = \(\frac{1}{2}\) AC (tính chất đường trung bình của tam giác)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 11 trang 156 SBT Toán 8 Tập 1
Bài tập 1.1 trang 156 SBT Toán 8 Tập 1
Bài tập 1.3 trang 157 SBT Toán 8 Tập 1
Bài tập 1 trang 155 SBT Toán 8 Tập 1
Bài tập 2 trang 155 SBT Toán 8 Tập 1
Bài tập 3 trang 155 SBT Toán 8 Tập 1
Bài tập 4 trang 156 SBT Toán 8 Tập 1
Bài tập 5 trang 156 SBT Toán 8 Tập 1
Bài tập 6 trang 156 SBT Toán 8 Tập 1
Bài tập 7 trang 156 SBT Toán 8 Tập 1
Bài tập 8 trang 156 SBT Toán 8 Tập 1
Bài tập 9 trang 156 SBT Toán 8 Tập 1
Bài tập 10 trang 156 SBT Toán 8 Tập 1
Bài tập 11 trang 156 SBT Toán 8 Tập 1
Bài tập 1.1 trang 156 SBT Toán 8 Tập 1
-


Chứng minh EF // BD biết tứ giác ABCD có O lầ giao điểm 2 đường chéo, đường thẳng qua O // vs BC cắt AB ở E
bởi ngọc trang
 31/05/2019
31/05/2019
Cho tứ giác ABCD, O là giao điểm của 2 đường chéo, đường thẳng qua O // vs BC cắt AB ở E. Đgt // CD qua O cắt AD ở F. CM: EF // BD.
Theo dõi (0) 1 Trả lời -


Cho hình thang ABCD đáy nhỏ CD. Từ D vẽ đgt // vs BC cắt AC tại m. Từ C vẽ đgt // vs AD cắt AB tại F. Qua F vẽ đgt // vs AC cắt BC tại D. CMR:
a, MP // AB
b, Gọi I là gđ của BD và CF. CMR: IP // CD
c, MP, CF, BD đồng quy
HELP ME1 THANKS CÁC BN TR'C NHA
Theo dõi (0) 1 Trả lời