Giải bài 8 tr 84 sách BT Toán lớp 8 Tập 2
Hình 7 cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC và BC.
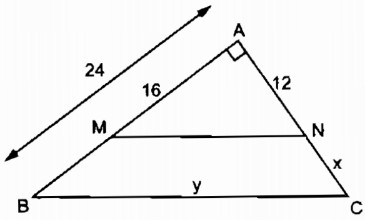
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
- Hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải chi tiết
Xét \(∆ ABC\) có \(MN // BC\) (gt)
Theo định lí Ta-lét ta có:
\(\displaystyle{{AM} \over {AB}} = {{AN} \over {AC}}\)
\(\displaystyle \Rightarrow AC = {{AB.AN} \over {AM}} = {{24.12} \over {16}} = 18\) (cm)
\( NC = AC - AN = 18 - 12 \)\(\,= 6 (cm)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AMN\), ta có:
\(M{N^2} = A{M^2} + A{N^2}\)
\(= {16^2} + {12^2} = 400 \)
\( \Rightarrow MN = 20\;(cm) \)
Xét \(∆ABC\) có \(MN // BC\) (gt)
Theo hệ quả định lí Ta-lét ta có:
\(\displaystyle {{AM} \over {AB}} = {{MN} \over {BC}}\)
\(\displaystyle \Rightarrow BC = {{MN.AB} \over {AM}} \)\(\,\displaystyle= {{20.24} \over {16}} = 30\; (cm)\)
Vậy \(x=6\,cm;y=30\,cm\).
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 6 trang 84 SBT Toán 8 Tập 2
Bài tập 7 trang 84 SBT Toán 8 Tập 2
Bài tập 9 trang 84 SBT Toán 8 Tập 2
Bài tập 10 trang 84 SBT Toán 8 Tập 2
Bài tập 11 trang 85 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2
-


Cho tam giác ABC, lấy M trên BC sao cho BM = 2CM
bởi Mận Art
 10/02/2020
10/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh tam giác ABC đồng dạng tam giác HBA. Từ đó suy ra AB^2 = BC × BH
bởi Tô Mai Phương
 14/04/2019
14/04/2019
Tam giác ABC vuông tại A có đường cao AH
1.Chứng minh tam giác ABC đồng dạng tam giác HBA. Từ đó suy ra AB^2 = BC × BH
2. Kẻ phân giác BD của góc ABC, D thuộc AC, BD cắt AH tại E Chứng minh rằng AB×HE=AD×HB
3.Chứng minh tam giác ADE cân
4. Kẻ DF vuông góc với BC, F thuộc BC. Giả sử AB = 3 BH tính tỉ số diện tích của tam giác HEF và tam giác HAC.Theo dõi (0) 6 Trả lời -


Tam giác MNP vuông tại M. Đường cao MH cắt phân giác NQ tại I.
a, C/m: △ MNP đồng dạng với △ HNM
b, C/m: MN2 = NH.NP
c, C/m: IH/IM = QM/QP
Theo dõi (0) 1 Trả lời


