Giải bài 10 tr 84 sách BT Toán lớp 8 Tập 2
Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q (h.9)
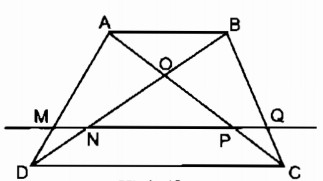
Chứng minh rằng MN = PQ.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Hệ quả định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
- Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
Xét \(\Delta ADB\) có \(MN // AB\) (gt)
Theo hệ quả định lí Ta-lét ta có:
\(\displaystyle{{DN} \over {DB}} = {{MN} \over {AB}}\) (1)
Xét \(\Delta ACB\) có \(PQ // AB\) (gt)
Theo hệ quả định lí Ta-lét ta có:
\(\displaystyle{{CQ} \over {CB}} = {{PQ} \over {AB}}\) (2)
Lại có: \(NQ // AB\) (gt)
\(AB // CD\) (gt)
Suy ra: \(NQ // CD\) (hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau).
Xét \(\Delta BDC\) có \(NQ // CD\) (chứng minh trên)
Theo định lí Ta-lét ta có:
\(\displaystyle {{DN} \over {DB}} = {{CQ} \over {CB}}\) (3)
Từ (1), (2) và (3) suy ra: \(\displaystyle {{MN} \over {AB}} = {{PQ} \over {AB}}\) hay \(MN = PQ.\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 8 trang 84 SBT Toán 8 Tập 2
Bài tập 9 trang 84 SBT Toán 8 Tập 2
Bài tập 11 trang 85 SBT Toán 8 Tập 2
Bài tập 12 trang 85 SBT Toán 8 Tập 2
Bài tập 13 trang 85 SBT Toán 8 Tập 2
Bài tập 14 trang 85 SBT Toán 8 Tập 2
Bài tập 15 trang 86 SBT Toán 8 Tập 2
Bài tập 16 trang 86 SBT Toán 8 Tập 2
Bài tập 2.1 trang 86 SBT Toán 8 Tập 2
-


Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng
Theo dõi (0) 1 Trả lời -


Chứng minh O là trung điểm của MN với O là giao điểm hai đường chéo của hình thang ABCD
bởi Lan Ha
 31/05/2019
31/05/2019
Bài 1: Cho hình thang ABCD ( AB//CD) . O là giao của 2 đường chéo , qua O kể đường thẳng // với 2 đáy cắt AD tại M, cắt BC tại N. CMR : O là trung điểm của MN
Bài 2: Cho \(\bigtriangleup{ABC}\) có S=120 cm2 . Đường cao AH , trung tuyến AM , gọi G là trọng tâm của \(\bigtriangleup{ABC}\). Đường thẳng đi qua G//BC cắt AB, AH, AC lần lượt tại E, I, F
a) Tính \(\dfrac{EF}{BC}\)và \(\dfrac{AI}{AH}\)
b) SAEF=?
Bài 3: Cho \(\diamond{ABCD}\) , đường thẳng đi qua A// với BC cắt BD tại E ; đường thẳng đi qua B // với AD cắt AC tại G
a) CM: EG//CD
b) Giả sử AB//CD . CM: AB2=CD.EG
Theo dõi (0) 1 Trả lời -


Tính độ dài đoạn thẳng DE, biết AD+EC=16cm và chu vi tam giác ABC bằng 75cm
bởi Nguyễn Hoài Thương
 31/05/2019
31/05/2019
cho tam giác ABC, G là trọng tâm. Qua G vẽ đường thẳng song song với cạnh AC, cắt các cạnh AB, BC lần lượt ở D và E. Tính độ dài đoạn thẳng DE, biết AD+EC=16cm và chu vi tam giác ABC bằng 75cm.
Theo dõi (0) 1 Trả lời



