Giải bài 45 tr 95 sách BT Toán lớp 8 Tập 2
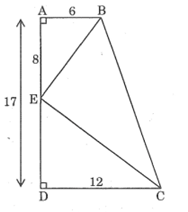
Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn thẳng AE = 8cm (h.31). Chứng minh góc BEC = 90°
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng.
Lời giải chi tiết
Ta có: \(AD = AE + DE\)
Suy ra: \(DE = AD - AE=17 - 8 = 9 (cm)\)
\(\displaystyle {{AB} \over {DE}} = {6 \over 9} = {2 \over 3}\)
\(\displaystyle {{AE} \over {DC}} = {8 \over {12}} = {2 \over 3}\)
\(\Rightarrow \displaystyle {{AB} \over {DE}} ={{AE} \over {DC}} = {2 \over 3}\)
Xét \(∆ ABE\) và \(∆ DEC\) có:
\(\widehat A = \widehat D = 90^\circ \)
\(\displaystyle {{AB} \over {DE}} = {{AE} \over {DC}}= {2 \over 3}\)
\(\Rightarrow ∆ ABE \backsim ∆ DEC \) (c.g.c)
\(\Rightarrow \widehat {ABE} = \widehat {DEC}\) (1)
Xét \(∆ ABE\) có \(\widehat A = 90^\circ\)
\( \Rightarrow \widehat {ABE} + \widehat {AEB} = 90^\circ \) (2)
Từ (1) và (2) suy ra: \( \widehat {DEC} + \widehat {AEB} = 90^\circ \)
Lại có: \(\widehat {AEB} + \widehat {BEC} + \widehat {DEC} = \widehat {AED} \)\(\,= 180^\circ \) (góc bẹt)
\(\Rightarrow \widehat {BEC} = 180^\circ - \left( {\widehat {AEB} + \widehat {DEC}} \right) \)\(\,= 180^\circ - 90^\circ = 90^\circ \)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 52 trang 85 SGK Toán 8 Tập 2
Bài tập 44 trang 95 SBT Toán 8 Tập 2
Bài tập 46 trang 95 SBT Toán 8 Tập 2
Bài tập 47 trang 95 SBT Toán 8 Tập 2
Bài tập 48 trang 95 SBT Toán 8 Tập 2
Bài tập 49 trang 96 SBT Toán 8 Tập 2
Bài tập 50 trang 96 SBT Toán 8 Tập 2
Bài tập 8.1 trang 96 SBT Toán 8 Tập 2
-


Chứng minh AD.AB=AN.AC?
bởi Thanh Vân
 21/05/2020
21/05/2020
Giúp mình với!!!(ಥ﹏ಥ)Mai mình phải kiểm tra hệ số 2 bài này rồi!!!ToT
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Ai giúp em với ạ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh \(\Delta HNM\) đồng dạng \( \Delta MNP\)?
bởi Nguyễn Nhung
 18/05/2020
18/05/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Cho tam giác ABC vuông tại A đường cao AH
bởi Văn Thắng
 17/05/2020
17/05/2020
a)chứng minh tam giác HBA đồng dạng tam giác ABC
b)tính BC,BH biết AB=9,AC=12
Theo dõi (0) 3 Trả lời -
ADMICRO


Cho tam giác ABC có AB=14cm, AC=21cm, AD là tia phân giác của góc A (D thuộc BC)
bởi Khánh Linh
 17/05/2020
17/05/2020
a) Biết BD=12cm. Tính độ dài đoạn DC, BC
b) qua D kẻ đường thẳng song song với AB, đường thẳng này cắt AC ở E. Tính độ dài DE
c) khi góc BAC=120 độ. Chứng minh rằng 1/AD=1/Ab+1/AC
Theo dõi (0) 0 Trả lời -


Chứng minh tam giác BMD đồng dạng với tam giác CND?
bởi Tâm Tâm
 15/05/2020
15/05/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tính AB, AC, BC biết tam giác ABC có MN//BC
bởi Lan
 13/05/2020
.
13/05/2020
. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh CD = AE . AD ?
bởi Oanh Nhat
 10/05/2020
10/05/2020
Cho tam giác ABC vuông tại A AB bé hơn AC Vẽ đường cao AH H thuộc BC Gọi D là điểm đối xứng với b qua h a chứng minh tam giác ABC đồng dạng tam giác hba b từ C kẻ đường thẳng vuông góc với tia AD cắt tia BC tại E
Chứng minh CD = AE nhân AD C
Chứng minh tam giác ABC đồng dạng tam giác ABC
tính diện tích tam giác dec biết AB = 6 cm AC = 8 cm b cắt cạnh AC tại k
Chứng minh k d là tia phân giác của góc hke
Theo dõi (0) 0 Trả lời


