Bài tập 24 trang 159 SBT Toán 8 Tập 1
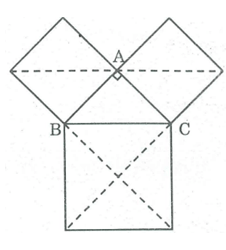
Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Hướng dẫn giải chi tiết
Gọi S là diện tích của tam giác ABC.
Hình vuông có cạnh AB được chia thành hai tam giác vuông cân bằng ΔABC nên diện tích hình vuông cạnh AB bằng 2S.
Hình vuông có cạnh AC được chia thành hai tam giác vuông cân bằng ΔABC nên diện tích hình vuông cạnh AB bằng 2S.
Hình vuông cạnh BC được chia thành bốn hình tam giác vuông cân bằng ΔABC nên có diện tích bằng 4S.
Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 22 trang 158 SBT Toán 8 Tập 1
Bài tập 23 trang 158 SBT Toán 8 Tập 1
Bài tập 2.1 trang 159 SBT Toán 8 Tập 1
Bài tập 2.2 trang 159 SBT Toán 8 Tập 1
Bài tập 2.3 trang 159 SBT Toán 8 Tập 1
Bài tập 12 trang 157 SBT Toán 8 Tập 1
Bài tập 13 trang 157 SBT Toán 8 Tập 1
Bài tập 14 trang 157 SBT Toán 8 Tập 1
Bài tập 15 trang 157 SBT Toán 8 Tập 1
Bài tập 16 trang 157 SBT Toán 8 Tập 1
Bài tập 17 trang 157 SBT Toán 8 Tập 1
Bài tập 18 trang 158 SBT Toán 8 Tập 1
Bài tập 19 trang 158 SBT Toán 8 Tập 1
Bài tập 20 trang 158 SBT Toán 8 Tập 1
Bài tập 21 trang 158 SBT Toán 8 Tập 1
Bài tập 22 trang 158 SBT Toán 8 Tập 1
Bài tập 23 trang 158 SBT Toán 8 Tập 1
Bài tập 24 trang 159 SBT Toán 8 Tập 1
Bài tập 2.1 trang 159 SBT Toán 8 Tập 1
-


Chứng minh chu vi tam giác FMC luôn không đổi
bởi Nguyen Kim Dung
 26/12/2019
cho hình vuông ABCD, M là một điểm bất kì thuộc cạnh BC trong nửa mo bờ AB chưas C dựng hình vuông AMHN qua M dựng đường thẳng d song song với AB cắt AH ở E AH cắt CD ở F BM=ND DF BM=FM cm chu vi tam giác FMC luôn không đổiTheo dõi (0) 0 Trả lời
26/12/2019
cho hình vuông ABCD, M là một điểm bất kì thuộc cạnh BC trong nửa mo bờ AB chưas C dựng hình vuông AMHN qua M dựng đường thẳng d song song với AB cắt AH ở E AH cắt CD ở F BM=ND DF BM=FM cm chu vi tam giác FMC luôn không đổiTheo dõi (0) 0 Trả lời -


Hình thành các công thức tính diện tích hình tam giác qua công thức tính diện tích hình chữ nhật
bởi Nguyễn Thị Thanh Thùy
 13/12/2019
Hình thành các công thức tính diện tích hình tam giác qua công thức tính diện tích hình chữ nhật
13/12/2019
Hình thành các công thức tính diện tích hình tam giác qua công thức tính diện tích hình chữ nhật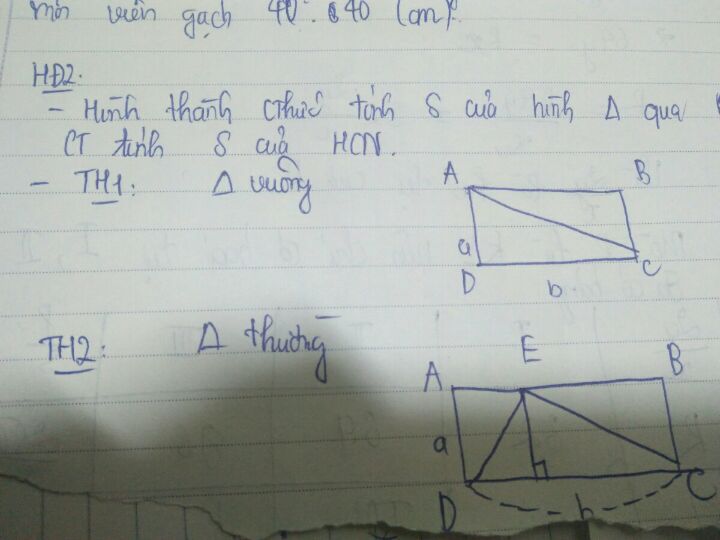 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời