Giải bài 23 tr 158 sách BT Toán lớp 8 Tập 1
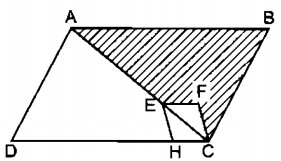
Trên hình 185, các tứ giác ABCD và EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC.
a. Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích.
b. ABCFE có phải là đa giác lồi không ? Vì sao ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) \( {S_{ABC}} = {S_{CDA}}\)
\({S_{EFC}} = {S_{CHE}}\)
\({S_{ABC}} - {S_{EFC}} = {S_{CDA}} - {S_{CHE}}\)
Hay \({S_{ABCFE}} = {S_{AEHD}}\)
b) Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
Lời giải chi tiết
a) Xét \(∆ ABC\) và \(∆ CDA\) có:
\(AB=CD\) ( vì \(ABCD\) là hình bình hành)
\(BC=AD\) ( vì \(ABCD\) là hình bình hành)
\(AC\) chung
\(\Rightarrow ∆ ABC = ∆ CDA \,(c.c.c)\)
\( \Rightarrow {S_{ABC}} = {S_{CDA}}\) (1)
Xét \(∆ EFC\) và \(∆ CHE\) có:
\(EF=HC\) (vì \(EFCH\) là hình bình hành)
\(FC=EH\) (vì \(EFCH\) là hình bình hành)
\(EC\) chung
\( \Rightarrow ∆ EFC = ∆ CHE\, (c.c.c)\)
\( \Rightarrow {S_{EFC}} = {S_{CHE}}\) (2)
Từ (1) và (2) suy ra:
\({S_{ABC}} - {S_{EFC}} = {S_{CDA}} - {S_{CHE}}\)
Hay \({S_{ABCFE}} = {S_{AEHD}}\)
b) Hình \(ABCFE\) không phải đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh \(CF.\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Bài 7/118 SGk
bởi Hoa Lan
 25/07/2018
25/07/2018
Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước là 1,2m và 2m.
Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không?
Bai nay trong sgk ak m,n minh k biet lam sao, bạn nap biet chi minh với nhé
Theo dõi (0) 2 Trả lời


