Giải bài 18 tr 28 sách BT Toán lớp 8 Tập 1
Cộng các phân thức khác mẫu thức:
a. \({5 \over {6{x^2}y}} + {7 \over {12x{y^2}}} + {{11} \over {18xy}}\)
b. \({{4x + 2} \over {15{x^3}y}} + {{5y - 3} \over {9{x^2}y}} + {{x + 1} \over {5x{y^3}}}\)
c. \({3 \over {2x}} + {{3x - 3} \over {2x - 1}} + {{2{x^2} + 1} \over {4{x^2} - 2x}}\)
d. \({{{x^3} + 2x} \over {{x^3} + 1}} + {{2x} \over {{x^2} - x + 1}} + {1 \over {x + 1}}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
\( \dfrac{A}{B}+\dfrac{C}{D}=\dfrac{AD}{BD}+\dfrac{CB}{DB}\)\(\,=\dfrac{AD+BC}{BD}\)
Lời giải chi tiết
a. \({5 \over {6{x^2}y}} + {7 \over {12x{y^2}}} + {{11} \over {18xy}}\)\( = {{30y} \over {36{x^2}{y^2}}} + {{21x} \over {36{x^2}{y^2}}} + {{22xy} \over {36{x^2}{y^2}}} = {{30y + 21x + 22xy} \over {36{x^2}{y^2}}}\)
b. \({{4x + 2} \over {15{x^3}y}} + {{5y - 3} \over {9{x^2}y}} + {{x + 1} \over {5x{y^3}}}\)\(\eqalign{ & = {{3{y^2}\left( {4x + 2} \right)} \over {45{x^3}{y^3}}} + {{5x{y^2}\left( {5y - 3} \right)} \over {45{x^3}{y^3}}} + {{9{x^2}\left( {x + 1} \right)} \over {45{x^3}{y^3}}} \cr & = {{12x{y^2} + 6{y^2} + 25x{y^3} - 15x{y^2} + 9{x^3} + 9{x^2}} \over {45{x^3}{y^3}}} = {{6{y^2} + 25x{y^3} - 3x{y^2} + 9{x^3} + 9{x^2}} \over {45{x^3}{y^3}}} \cr} \)
c. \({3 \over {2x}} + {{3x - 3} \over {2x - 1}} + {{2{x^2} + 1} \over {4{x^2} - 2x}}\)\( = {3 \over {2x}} + {{3x - 3} \over {2x - 1}} + {{2{x^2} + 1} \over {2x\left( {2x - 1} \right)}}\)
\(\eqalign{ & = {{3\left( {2x - 1} \right)} \over {2x\left( {2x - 1} \right)}} + {{2x\left( {3x - 3} \right)} \over {2x\left( {2x - 1} \right)}} + {{2{x^2} + 1} \over {2x\left( {2x - 1} \right)}} = {{6x - 3 + 6{x^2} - 6x + 2{x^2} + 1} \over {2x\left( {2x - 1} \right)}} \cr & = {{8{x^2} - 2} \over {2x\left( {2x - 1} \right)}} = {{2\left( {4{x^2} - 1} \right)} \over {2x\left( {2x - 1} \right)}} = {{\left( {2x + 1} \right)\left( {2x - 1} \right)} \over {x\left( {2x - 1} \right)}} = {{2x + 1} \over x} \cr} \)
d. \({{{x^3} + 2x} \over {{x^3} + 1}} + {{2x} \over {{x^2} - x + 1}} + {1 \over {x + 1}}\)\( = {{{x^3} + 2x} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} + {{2x} \over {{x^2} - x + 1}} + {1 \over {x + 1}}\)
\(\eqalign{ & = {{{x^3} + 2x} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} + {{2x\left( {x + 1} \right)} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} + {{{x^2} - x + 1} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} \cr & = {{{x^3} + 2x + 2{x^2} + 2x + {x^2} - x + 1} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = {{{x^3} + 3{x^2} + 3x + 1} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = {{{{\left( {x + 1} \right)}^3}} \over {\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} \cr & = {{{{\left( {x + 1} \right)}^2}} \over {{x^2} - x + 1}} \cr} \)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Thực hiện phép tính: \( \dfrac{5xy-4y}{2x^{2}y^{3}}+\dfrac{3xy+4y}{2x^{2}y^{3}}\)
bởi Khanh Đơn
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Thực hiện phép tính: \(\dfrac{{2x}}{{{x^2} + 4x + 4}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{2 - x}}{{{x^2} + 4x + 4}}\)
bởi An Duy
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Thực hiện phép cộng: \(\dfrac{{y - 12}}{{6y - 36}} + \dfrac{6}{{{y^2} - 6y}}\)
bởi thúy ngọc
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -
ADMICRO

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Thực hiện phép cộng: \(\dfrac{{3x + 1}}{{7{x^2}y}} + \dfrac{{2x + 2}}{{7{x^2}y}}\)
bởi Trịnh Lan Trinh
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


\(A=\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+ ...+\dfrac{1}{120}\)
Theo dõi (0) 0 Trả lời -


Đây là bài nâng cao, nên khá khó giải. Hy vọng có bạn nào đó giải được.
Theo dõi (1) 0 Trả lời -


Tìm gtnn của biểu thức B=x^2 y^2. Biết x+ y=2
bởi Giang Hoàng Thị
 21/03/2020
21/03/2020
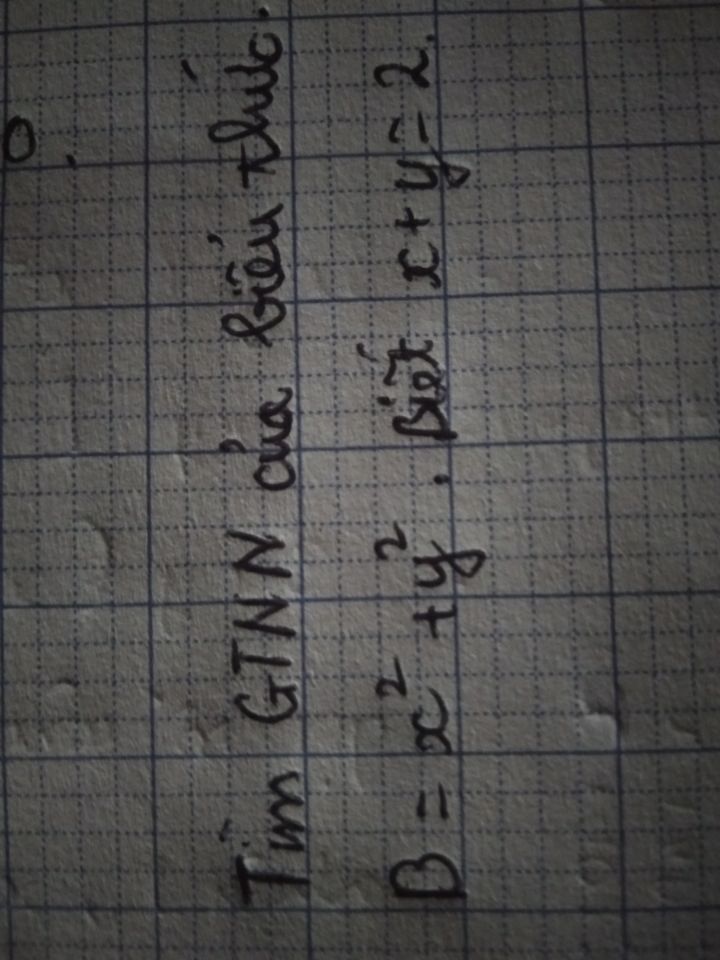 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính tổng 1/1.3 1/3.5 1/5.7 ... 1/(2n-1)(2n 1)
bởi Quang Phan
 12/03/2020
12/03/2020
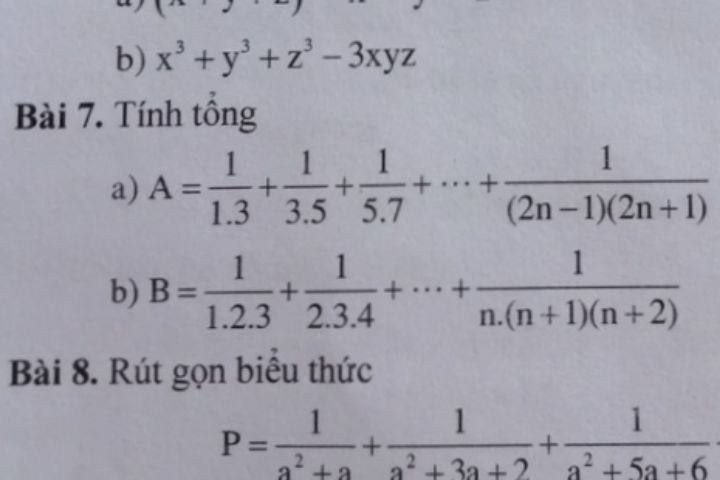 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giá trị biểu thức đại số
bởi Uyên Phan Võ Tú
 13/02/2020
13/02/2020
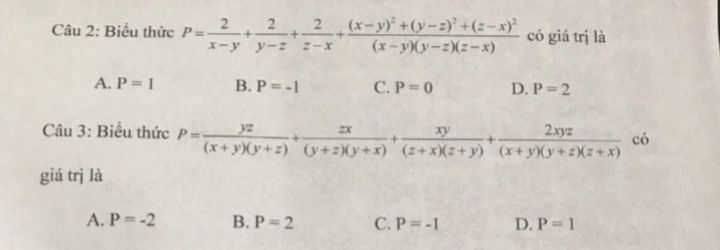 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính 8x+5/3-x 3x-1/2x-6
bởi Lợi Không Trắng
 24/12/2019
24/12/2019
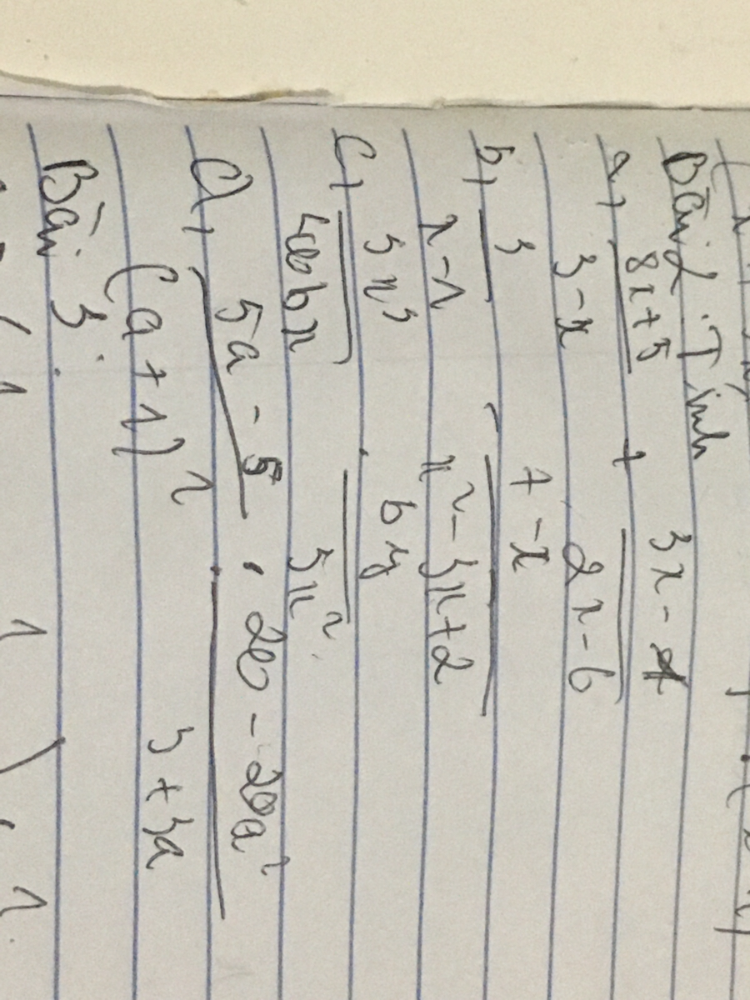 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời



