Giải bài 4.43 trang 69 SBT Toán 7 Kết nối tri thức tập 1
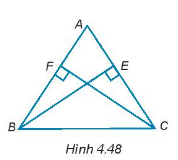
Tam giác ABC có 2 đường chéo BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.
Hướng dẫn giải chi tiết
Phương pháp giải:
Chứng minh \(\Delta AEB = \Delta AFC\left( {g - c - g} \right)\), từ đó suy ra 2 cạnh tương ứng bằng nhau.
Lời giải chi tiết:
Xét \(\Delta AEB\) và \(\Delta AFC\) có:
\(\widehat {AEB} = \widehat {AFC}( = {90^0})\\BE = CF\left( {gt} \right)\\\widehat {ACF} = \widehat {ABE}(= {90^0} - \widehat A)\\ \Rightarrow \Delta AEB = \Delta AFC\left( {g - c - g} \right)\\ \Rightarrow AB = AC\) ( 2 cạnh tương ứng)
Vậy tam giác ABC cân tại A.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 4.41 trang 68 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.42 trang 68 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.44 trang 69 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.45 trang 69 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.46 trang 69 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.47 trang 70 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.48 trang 70 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.49 trang 70 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.50 trang 70 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


