Giải bài 4.39 trang 87 SGK Toán 7 Kết nối tri thức tập 1
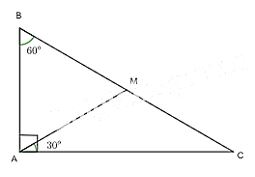
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
Hướng dẫn giải chi tiết Giải bài 4.39
Phương pháp giải
a) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ suy ra góc A bằng góc C.
b) Chứng minh tam giác ABM cân có 1 góc bằng 60 độ
c) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ để tính số đo 3 góc từ đó suy ra tam giác đều
Lời giải chi tiết
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 4.37 trang 87 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.38 trang 87 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 1 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 2 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 3 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 4 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 5 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 6 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 7 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.51 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.52 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.53 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.54 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.55 trang 73 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.56 trang 73 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.57 trang 73 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.58 trang 74 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.59 trang 74 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.60 trang 74 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.