Hó¯Ã£ng dä¨n GiäÈi bû i täÙp ToûÀn 7 CûÀnh diãu Bû i täÙp cuãi chó¯óÀng 7 giû¤p cûÀc em hãc sinh nä₤m vã₤ng phó¯óÀng phûÀp giäÈi bû i täÙp vû ûÇn luyãn tãt kiä¢n thãˋc.
-
GiäÈi bû i 1 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû°: \(\widehat A = 42^\circ ,\widehat B = 37^\circ \).
a) TûÙnh \(\widehat C\).
b) So sûÀnh áã dû i cûÀc cäÀnh AB, BC, CA.
-
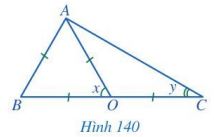
GiäÈi bû i 2 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Tû˜m cûÀc sã áo x, y trong Hû˜nh 140.
-
GiäÈi bû i 3 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
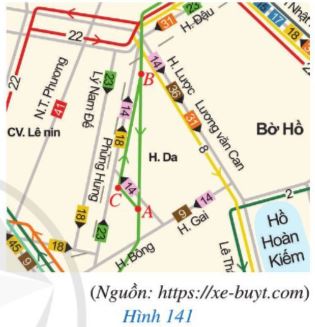
BäÀn Hoa áûÀnh däËu ba vã trûÙ A, B, C trûˆn mãt phäÏn sóÀ áã xe buû§t ã Hû Nãi nám 2021 vû xem xe buû§t cû° thã ái nhó¯ thä¢ nû o giã₤a hai vã trûÙ A vû B. áó¯Ã£ng thãˋ nhäËt ái t㨠A áä¢n C vû ái tiä¢p t㨠C áä¢n B, áó¯Ã£ng thãˋ hai ái t㨠B áä¢n A (Hû˜nh 141). Theo em, áó¯Ã£ng nû o ái dû i hóÀn? Vû˜ sao?
-
GiäÈi bû i 4 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho hai tam giûÀc ABC vû MNP cû°: AB = MN, BC = NP, CA = PM. Gãi I vû K läÏn ló¯Ã£Èt lû trung áiãm cãÏa BC vû NP. Chãˋng minh AI = MK.
- VIDEOYOMEDIA
-
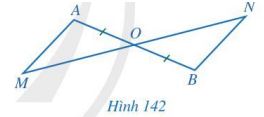
GiäÈi bû i 5 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho Hû˜nh 142 cû° O lû trung áiãm cãÏa áoäÀn thä°ng AB vû O näÝm giã₤a hai áiãm M, N. Chãˋng minh:
a) Nä¢u OM = ON thû˜ AM // BN;
b) Nä¢u AM // BN thû˜ OM = ON.
-
GiäÈi bû i 6 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cûÂn täÀi A cû° \(\widehat {ABC} = 70^\circ \). Hai áó¯Ã£ng cao BD vû CE cä₤t nhau täÀi H.
a) TûÙnh sã áo cûÀc gû°c cûýn läÀi cãÏa tam giûÀc ABC.
b) Chãˋng minh BD = CE.
c) Chãˋng minh tia AH lû tia phûÂn giûÀc cãÏa gû°c BAC.
-
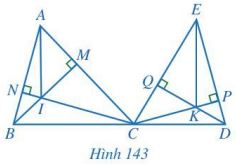
GiäÈi bû i 7 trang 119 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho hai tam giûÀc nhãn ABC vû ECD, trong áû° ba áiãm B, C, D thä°ng hû ng. Hai áó¯Ã£ng cao BM vû CN cãÏa tam giûÀc ABC cä₤t nhau täÀi I, hai áó¯Ã£ng cao CP vû DQ cãÏa tam giûÀc ECD cä₤t nhau täÀi K (Hû˜nh 143). Chãˋng minh AI // EK.
-
GiäÈi bû i 8 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
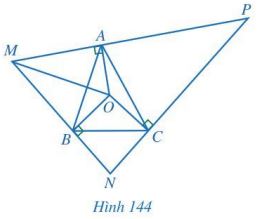
Cho tam giûÀc ABC cû° O lû giao áiãm cãÏa ba áó¯Ã£ng trung trãÝc. Qua cûÀc áiãm A, B, C läÏn ló¯Ã£Èt kä£ cûÀc áó¯Ã£ng thä°ng vuûÇng gû°c vãi OA, OB, OC, hai trong ba áó¯Ã£ng áû° läÏn ló¯Ã£Èt cä₤t nhau täÀi M, N, P (Hû˜nh 144). Chãˋng minh:
a) \(\Delta OMA = \Delta OMB\) vû tia MO lû tia phûÂn giûÀc cãÏa gû°c NMP;
b) O lû giao áiãm cãÏa ba áó¯Ã£ng phûÂn giûÀc cãÏa tam giûÀc MNP.
-
GiäÈi bû i 9 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû° G lû trãng tûÂm, H lû trãÝc tûÂm, I lû giao áiãm cãÏa ba áó¯Ã£ng phûÂn giûÀc, O lû giao áiãm cãÏa ba áó¯Ã£ng trung trãÝc. CûÀc áiãm A, G, H, I, O phûÂn biãt. Chãˋng minh räÝng:
a) Nä¢u tam giûÀc ABC cûÂn täÀi A thû˜ cûÀc áiãm A, G, H, I, O cû¿ng näÝm trûˆn mãt áó¯Ã£ng thä°ng;
b) Nä¢u cûÀc áiãm A, H, I cû¿ng näÝm trûˆn mãt áó¯Ã£ng thä°ng thû˜ tam giûÀc ABC cûÂn täÀi A.
-
GiäÈi bû i 10 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
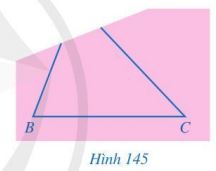
BäÀn Hoa vä§ tam giûÀc ABC lûˆn tã giäËy sau áû° cä₤t mãt phäÏn tam giûÀc ã phûÙa gû°c A (Hû˜nh 145). BäÀn Hoa áã bäÀn Hû¿ng: KhûÇng vä§ áiãm A, lû m thä¢ nû o tû˜m áó¯Ã£Èc áiãm D trûˆn áó¯Ã£ng thä°ng BC sao cho khoäÈng cûÀch t㨠D áä¢n áiãm A lû nhã nhäËt? Em hûÈy giû¤p bäÀn Hû¿ng tû˜m cûÀch vä§ áiãm D vû giäÈi thûÙch cûÀch lû m cãÏa mû˜nh?
-
GiäÈi bû i 11 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû° hai áó¯Ã£ng trung tuyä¢n AM vû BN cä₤t nhau täÀi G. Khi áû°
A.\(AM = 2GM\).
B.\(AM = 2AG\).
C.\(GA = 3GM\).
D.\(GA = 2GM\).
-
GiäÈi bû i 12 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cûÂn täÀi A cû° \(\widehat {BAC} = 40^\circ \). Hai áó¯Ã£ng trung trãÝc cãÏa hai cäÀnh AB, AC cä₤t nhau täÀi O. Khi áû°
A.\(OA = OB = AB\).
B.\(OA = OB = OC\).
C.\(OB = OC = BC\).
D.\(OC = OA = AC\).
-
GiäÈi bû i 13 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû° BC > AC, I lû giao áiãm cãÏa hai áó¯Ã£ng phûÂn giûÀc gû°c A vû gû°c B. Khi áû°
A.\(\widehat {ICA} = \widehat {ICB}\).
B.\(\widehat {IAC} = \widehat {IBC}\).
C.\(\widehat {ICA} > \widehat {ICB}\).
D.\(\widehat {ICA} < \widehat {IBC}\).
-
GiäÈi bû i 14 trang 120 SGK ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc nhãn ABC cû° AB < AC. Hai áó¯Ã£ng cao AD vû CE cä₤t nhau täÀi H. Khi áû°
A.\(\widehat {HAB} = \widehat {HAC}\).
B.\(\widehat {HAB} > \widehat {HAC}\).
C.\(\widehat {HAB} = \widehat {HCB}\).
D.\(\widehat {HAC} = \widehat {BAC}\).
-
GiäÈi bû i 99 trang 98 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho hai tam giûÀc ABC vû MNP cû° \(\widehat {ACB} = \widehat {MPN}\), \(\widehat {ACB} = \widehat {MPN}\). CäÏn thûˆm mãt áiãu kiãn áã tam giûÀc ABC vû tam giûÀc MNP bäÝng nhau theo tró¯Ã£ng hãÈp gû°c ã cäÀnh ã gû°c lû :
A. AC = MP;
B. AB = MN;
C. BC = NP;
D. AC = MN.
-
GiäÈi bû i 100 trang 98 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû° \(\widehat {BAC} = 110^\circ \). CûÀc áó¯Ã£ng trung trãÝc cãÏa AB vû AC cä₤t cäÀnh BC läÏn ló¯Ã£Èt täÀi E vû F. Khi áû°, sã áo gû°c EAF bäÝng:
A. 20ô¯;
B. 30ô¯;
C. 40ô¯;
D. 50ô¯.
-
GiäÈi bû i 101 trang 98 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
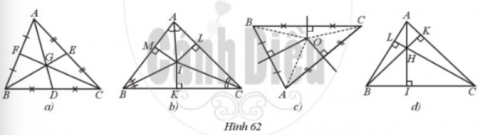
Trong cûÀc hû˜nh 62a, 62b, 62c, 62d, hû˜nh nû o cû° áiãm cûÀch áãu cûÀc áãnh cãÏa tam giûÀc áû°? Vû˜ sao?
-
GiäÈi bû i 102 trang 98 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC vû áiãm G näÝm trong tam giûÀc. Chãˋng minh: Nä¢u diãn tûÙch cûÀc tam giûÀc GAB, GBC vû GCA bäÝng nhau thû˜ G lû trãng tûÂm cãÏa tam giûÀc áû°.
-
GiäÈi bû i 103 trang 98 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû° ba gû°c nhãn, AB < AC < BC. CûÀc tia phûÂn giûÀc cãÏa gû°c A vû gû°c C cä₤t nhau täÀi O. Gãi F lû hû˜nh chiä¢u cãÏa O trûˆn BC; H lû hû˜nh chiä¢u cãÏa O trûˆn AC. LäËy áiãm I trûˆn áoäÀn FC sao cho FI = AH. Chãˋng minh:
a) OC vuûÇng gû°c vãi FH;
b) Tam giûÀc OAI lû tam giûÀc cûÂn;
c) Tam giûÀc BAI lû tam giûÀc cûÂn.
-
GiäÈi bû i 104 trang 99 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cû° AB < AC, M lû trung áiãm cãÏa BC. Trûˆn tia áãi cãÏa tia MA läËy áiãm E sao cho ME = MA.
a) Chãˋng minh AC = EB vû AC song song vãi EB.
b) Gãi I lû mãt áiãm trûˆn AC, K lû mãt áiãm trûˆn EB sao cho AI = EK. Chãˋng minh ba áiãm I, M, K thä°ng hû ng.
c) T㨠E kä£ EH vuûÇng gû°c vãi BC täÀi H. Cho biä¢t \(\widehat {HBE} = 50^\circ ;\widehat {MEB} = 25^\circ \). TûÙnh sã áo cûÀc gû°c HEB vû HEM.
-
GiäÈi bû i 105 trang 99 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC cûÂn täÀi A cû° cûÀc áó¯Ã£ng cao BD vû CE cä₤t nhau täÀi H.
a) Chãˋng minh ãADB = ãAEC.
b) Chãˋng minh tam giûÀc HDE lû tam giûÀc cûÂn.
c) So sûÀnh HB vû HD.
d) Gãi M lû trung áiãm cãÏa HC, N lû trung áiãm cãÏa HB, I lû giao áiãm cãÏa BM vû CN. Chãˋng minh ba áiãm A, H, I thä°ng hû ng.
-
GiäÈi bû i 106 trang 99 SBT ToûÀn 7 CûÀnh diãu täÙp 2 - CD
Cho tam giûÀc ABC vuûÇng täÀi A cû° AB < AC. Vä§ AD lû tia phûÂn giûÀc cãÏa gû°c BAC (D ã BC). Trûˆn AC läËy áiãm E sao cho AE = AB.
a) Chãˋng minh \(\widehat {ABD} = \widehat {AED}\)
b) Tia ED cä₤t AB täÀi F. Chãˋng minh AC = AF.
c) Gãi G lû trung áiãm cãÏa DF; AD cä₤t CF täÀi H vû cä₤t CG täÀi I. Chãˋng minh DI = 2IH.